précédent | suivant | table des matières

Exercices de programmation : tableaux

Tabeaux à 1 dimension
Tabeaux à 2 dimensions

Tableaux à une dimension.

Ecrire la définition d'une méthode qui initialise les éléments d’un tableau d’entiers à 0.
Ecrire la définition d'une méthode qui affiche le contenu d’un tableau à la console. On écrira deux versions , une qui affiche tous les éléments du tableau, l'autre qui affiche que les n premiers éléments du tableau.
Ecrire la définition d'une méthode qui retourne la chaîne de caractères "[", les éléments du tableau séparés par des "," et "]". On écrira deux versions , une qui prend en compte tous les éléments du tableau, l'autre qui ne prend en compte que les n premiers éléments du tableau.
Ecrire la définition d'une méthode qui augmente de 1 tous les éléments d’un tableau.
Ecrire la définition d'une méthode qui, pour tous les éléments d’un tableau d’entiers, affiche si cet élément est pair ou non.
Ecrire la définition d'une méthode calcule la somme des éléments d’un tableau. On écrira deux versions , une qui prend en compte tous les éléments du tableau, l'autre qui ne prend en compte que les n premiers éléments du tableau.
Ecrire une séquence d’instructions qui calcule le nombre d’éléments pairs dans un tableau d’entiers. On écrira deux versions , une qui prend en compte tous les éléments du tableau, l'autre qui ne prend en compte que les n premiers éléments du tableau.
Ecrire une séquence d’instructions qui calcule le maximum des éléments d’un tableau d’entiers. On écrira deux versions , une qui prend en compte tous les éléments du tableau, l'autre qui ne prend en compte que les n premiers éléments du tableau.
Ecrire une séquence d’instructions qui calcule si un tableau d’entiers est ordonné dans l’ordre croissant. On écrira deux versions , une qui prend en compte tous les éléments du tableau, l'autre qui ne prend en compte que les n premiers éléments du tableau.
Ecrire la définition de deux méthodes qui ordonnent les n premiers éléments d'un tableau d'entiers par ordre croissant, en utilisant les algorithmes suivants :
- Insertion : on suppose que la partie de tableau qui va de l'indice 0 à l'indice i est ordonnée. On insère alors l'élément d'indice i+1 dans cette partie ordonnée. on obtient alors une partie qui va de 0 à i+1 qui est ordonnée.
- Sélection/échange : On cherche le plus petit élément dans la partie qui va de l'indice i à l'indice n-1, puis on échange cet élément avec l'élément d'indice i. On recommence en faisant varier i.
Soit t un tableau d'entiers. Une série dans t est une suite d'éléments consécutifs et égaux de t. Ecrire une séquence d'instruction qui calcule l'indice du premier élément et la longueur de la plus longue série de t. exemple :
```
int [] t = {1, 1, 2, 2, 2, 9, 9, 9, 9, 2, 2, 3};
```
Alors la plus longue série commence à l'indice 5 et a pour longueur 4. On écrira deux versions , une qui prend en compte tous les éléments du tableau, l'autre qui ne prend en compte que les n premiers éléments du tableau.
Ecrire la définition d'une méthode qui comprime un tableau d'entiers. Pour réaliser la compression, on remplacera toute suite de n fois la valeur a par n suivi de a;
```
int [] t = {1, 1, 2, 2, 2, 9, 9, 9, 9, 2, 2, 3};
```
est comprimé en :
```
int [] t1 = {2, 1, 3, 2, 4, 9, 2, 2, 1, 3};
```
On écrira deux versions , une qui prend en compte tous les éléments du tableau, l'autre qui ne prend en compte que les n premiers éléments du tableau.
Ecrire la définition d'une méthode qui retourne l'indice de la première occurrence de l'entier a dans un tableau qui contient n éléments entiers. Cette méthode retourne -1 si l'entier a ne se trouve pas dans la tableau.

Même question que la précédente, en supposant que la tableau est ordonné par ordre croissant.
Ecrire la définition d'une méthode qui retourne l'élément médian d'un tableau d'entiers. L'élément médian est l'élément qui se trouverait au milieu du tableau si celui-ci était ordonné. On écrira deux versions , une qui prend en compte tous les éléments du tableau, l'autre qui ne prend en compte que les n premiers éléments du tableau.
Soit t un tableau de n entiers (n <= t.length).
- Ecrire la définition d'une méthode qui ajoute un élément à l'indice i dans le tableau, si c'est possible, et lève une exception sinon.
- Ecrire la définition d'une méthode qui enlève l'élément d'indice i du tableau, si c'est possible, et lève une exception sinon.
Nous supposons que le tableau t de n+1 nombres réels est le tableau des coefficients d'un polynome de degré n. Définir une méthode qui a en paramètre le tableau t et un nombre réel x, et qui retourne la valeur du polynome : xⁿ×t_n+x^n-1×t_n-1+...+x⁰×t₀. On utilisera la méthode de Méthode de Ruffini-Horner.

Programmer le crible d’Erathosthène pour calculer l’ensemble des nombres premiers inférieurs à 1000.
Définir une méthode qui retourne un tableau constitué des éléments du tableau d'entiers t. Dans le tableau retourné, chaque élément n'a qu'une seule occurrence.
Définir une méthode qui inverse l'ordre des éléments du tableau d'entiers en paramètre.
Définir une méthode qui retourne le tableau obtenu par concaténation des deux tableaux d'entiers en paramètres.
Définir une méthode qui modifie de façon aléatoire l'ordre des éléments du tableau d'entiers en paramètre. On écrira deux versions , une qui prend en compte tous les éléments du tableau, l'autre qui ne prend en compte que les n premiers éléments du tableau.
Supposons que deux tableaux de n éléments réels représentent deux vecteurs. Ecrire la définition d'une méthode qui retourne le produit scalaire de ces deux vecteurs. La valeur retournée est t1₀×t2₀+ ... +t1_n-1×t2_n-1.
Le langage Python définit l'opérateur slice sur les listes.Si l est une liste, l[d:f] est une liste constituée de tous les éléments de l qui vont de l'indice d (inclus) à l'indice f (exclu). Ecrire la définition d'une méthode slice qui a le même sens pour les tableaux à une dimension en Java.
Un diviseur de n qui est différent de n est appelé diviseur strict de n. Ecrire la définition d'une méthode qui retourne un tableau contenant tous les diviseurs stricts de n.

Un nombre abondant est un nombre dont la somme de ses diviseurs stricts est supérieure au nombre. Ecrire la définition d'une méthode qui énumères tous les nombres abondants inférieurs à 100.

Un nombre parfait est un nombre dont la somme de ses diviseurs stricts est égales au nombre. Ecrire la définition d'une méthode qui énumères tous les nombres parfaits inférieurs à 1000.

Deux nombres n et m sont amicaux si la somme de ses diviseurs stricts de n est égale à m, et la somme de ses diviseurs stricts de m est égale à n. Ecrire la définition d'une méthode qui énumères tous les couples de nombres amicaux inférieurs à 5000.
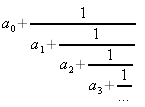
$a_{0}+{1}over{a_{1}+{1}over{a_{2}+{1}over{a_{3}+{1}over{...}}}}$

Un tableau a contient les coefficients intervenant dans une fraction continue.

Ecrire la définition d'une méthode qui retourne la valeur de la fraction continue calculée avec les coefficients contenus dans a.

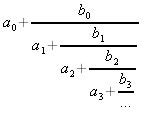
$a_{0}+{b_{0}}over{a_{1}+{b_{1}}over{a_{2}+{b_{2}}over{a_{3}+{b_{3}}over{...}}}}$

Un tableau a et un tableau b contiennent les coefficients intervenant dans une fraction continue généralisée.

Ecrire la définition d'une méthode qui retourne la valeur de la fraction continue calculée avec les coefficients contenus dans a et b.

Ecrire la définition d'une méthode qui calcule le tableau des coefficients pour un paramètre BigDecimal d, avec au maximum n termes. (voir ici)
Un arbre binaire ordonné horizontalement est défini par : tout noeud de l’arbre binaire a une valeur plus grande que la valeur de chacun de ses fils. Un arbre binaire ordonné horizontalement peut être représenté dans un tableau :
- La racine est à l’indice 0.
- L’élément à l’indice i est le père de l’élément à l’indice 2×i+1 s’il existe, et le père de l’élément de rang 2×i+2s’il existe.
Cette structure de tableau se nomme un tas
Exemple :
- Ajouter un élément dans le tas consiste à ajouter un élément en fin du tableau représentant le tas, puis à le remonter à sa place dans l’arbre et donc dans le tableau.
- Retirer un élément du tas, c’est retirer le premier élément, puis le remplacer par le dernier élément du tableau, et on descend cet élément dans l’arbre et donc dans le tableau.
Définir ces deux méthodes.
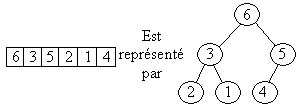
Une suite de Skolem est constituée d'entiers de 1 à n répétés deux fois. De plus, chaque entier i de la suite est à une distance i du même entier dans la suite. On vérifiera que la suite suivante est une suite de Skolem :
```
4, 1, 1, 5, 4, 2, 3, 2, 5, 3
```
On démontre qu'il n'existe des suites de Skolem que pour n tel que n%4==0 ou (n-1)%4==0.
- Ecrire la définition d'une méthode qui retourne true si un tableau d'entiers en paramètre contient une suite de Skolem et false sinon.
- Ecrire la définition d'une méthode qui retourne un tableau contenant une suite de Skolem pour un n donné, si c'est possible, et null sinon. A chaque appel la méthode ne retourne pas en général la même suite.
Une suite de Langford est constituée d'entiers de 1 à n répétés deux fois. De plus, chaque entier i de la suite est à une distance i+1 du même entier dans la suite.

Tableaux à deux dimensions.

Ecrire une séquence d’instructions qui initialise les éléments d’un tableau d’entiers à 2 dimensions (n et m) à 0.
Ecrire une séquence d’instructions qui initialise les éléments de la diagonale d’un tableau d’entiers à 2 dimensions (n et m) à 1.
Ecrire une séquence d’instructions qui affiche les éléments d’un tableau d’entiers à 2 dimensions (n et m). Chaque ligne du tableau est affichée sur une ligne de la console.
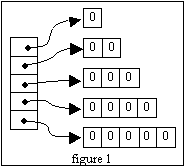
Ecrire une séquence d’instructions qui construit le tableau d'entiers (figure 1) :
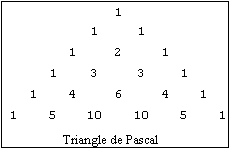
Ecrire la définition d'une méthode qui affiche le triangle de Pascal au rang n. On commencera par construire un tableau d'entiers contenant les valeurs du triangle de Pascal.
Exemple pour n=5 :
Ecrire la definition d'une méthode qui retourne le transposé d'un tableau d'entiers à 2 dimensions (n et m). Le transposé tt d'un tableau t est tel que pour tout i et j on a tt[i][j] == t[j][i].
Ecrire la definition d'une méthode qui retourne le tableau à deux dimensions (n, o) représentant le produit de deux matrices données en paramètre(n, m) et (n, o). Si le produit ne peut pas être calculé, on lèvera une exception. l'élément de ran i et j du résultat est : t1_i,0×t2_0,j+ t1_i,1×t2_1,j + ... +t1_i,m-1×t2_{m-1, j}.
Ecrire la definition d'une méthode qui retourne le tableau à deux dimensions (n×m, 2) représentant le produit cartésien de deux tableaux d'entiers à une dimension (n) et (m). Exemple :
```
int [] a = {1, 2, 3};
int [] b = {10, 11};
```
Alors produitCartesien(a,b) retourne le tableau :
```
 {{1,10},{1,11},
  {2,10},{2,11},
  {3,10},{3,11}
 }
```

haut de la page