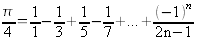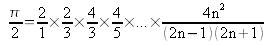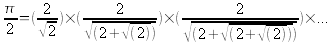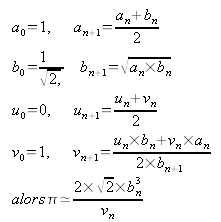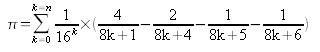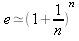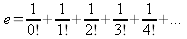précédent | suivant | table des matières

Exercices de programmation : nombres

Pourquoi les expressions suivantes sont-elles illégales ?
```
++i--
12 = 11+1
12 == 11+1 && 12
```

Parenthéser et évaluer les expressions suivantes.

int a, b, c ;
a = 1-+-1 
a = a+++a ;
a = b = c ;
a = a>5 ? c : 10 ; 
a = 7+3*6/2-1 ;
a = 2%2+2*2-2/2 ;
a = 3*9*(3+9*3/3) ;

Quelle(s) expression(s) correspond(ent) à la formule mathématique y = ax³+7 ?

y = a*x*x*x+7
y = a*x*x*(x+7)
y = (a*x)*x*(x+7)
y == a*x*x*x+7
y == a*x*x*x+7
y = a*(x*x*x)+7

Quelle est la valeur de a après chacune des instructions suivantes ?
```
short a = 215 ;
a = a*a*a*a ;
a += 10733022 ;
++a
```
Quelles sont les valeurs de a et b après chacune des instructions suivantes ?
```
int a = 215, b = 150, c ;
c = a ;
a = b ;
b = c ;
```
Quelles sont les valeurs de a et b après chacune des instructions suivantes ?
```
int a = 215, b = 150 ;
a = a - b ;
b = a + b ;
a = b - a ;
```

La séquence suivante énumère 10 entiers aléatoires, compris entre 0 et 1000 (exclu) :

Random rd = new Random();
for (int i = 0; i<10; ++i){
    int a = rd.nextInt(1000);
}

Dans la séquence suivante, remplacer la partie jaune par du code qui permet de calculer :

La somme des nombres.
Le produit des nombres.
Le maximum des nombres.

Random rd = new Random();
int res =                 ;
for (int i = 0; i<10; ++i){
    int a = rd.nextInt(1000);
    res =                 ;
}

Donner une expression qui est vraie si le n^ième bit d'un entier long est à 1 et fausse sinon.
Pour calculer la surface d’un triangle dont on connaît les longueurs des trois cotés ( a, b et c), on peut utiliser la formule de Heron :
```
p = (a+b+c)/2
s = sqrt(p*(p-a)*p-b)*(p-c))
```
Ecrire deux définitions de méthode qui calculent la surface d’un triangle connaissant la longueur de ses trois cotés. Une méthode utilise des double et l’autre des float .
Faire le test suivant :
```
   System.out.println(heronD(12345678.,  12345678.,  1.));
   System.out.println(heronF(12345678.F, 12345678.F, 1.F));

   System.out.println(heronD(1234567.,  1234567.,  1.));
   System.out.println(heronF(1234567.F, 1234567.F, 1.F));
```
Expliquer les résultats.
Ecrire une séquence d’instructions qui permet à l’ordinateur de deviner un nombre compris ente 1 et 16 choisi par l’utilisateur. L’ordinateur pose des questions du style « le nombre est-il <= à 7 », et l’utilisateur répond par « oui » ou « non ».
Définir les méthodes qui calculent :
- La somme des n premiers entiers.
- La somme des carrés de n premiers entiers.
- La somme des cubes de n premiers entiers.
Un nombre premier est un nombre qui n'est divisible que par 1 et par lui même. Ecrire la définition d'une méthode qui retourne true si le nombre n en paramètre est premier et false sinon.

Ecrire la définition d'une méthode qui retourne la somme des chiffres du nombre n écrit dans la base b. Exemple :
```
sommeChifres(63, 10) = 9
sommeChifres(63, 2) = 6
```
Un nombre de Smith est un nombre qui est tel que la somme de ses chiffres est égale à la somme des chiffres de tous ses facteurs premiers. Ecrire la définition d'une méthode qui retourne true si le nombre n en paramètre est un nombre de Smith et false sinon. Exemple :
```
estSmith(666, 10) = true
estSmith(666, 2) = false
estSmith(4937775, 10) = true
estSmith(4937775, 2)  = true
```
Pour calculer la racine carrée de a, l'algorithme de Newton ( aussi connu depuis l'antiquité sous le nom d'algorithme de babylone ou d'algorithme de Héron d'alexandrie) énumère les éléments de la suite :
```
  x₀ = a/2
  x_n+1 = 1/2×(x_n+a/x_n)
```
- Ecrire la définition d'une méthode qui calcule la racine carrée de a en calculant n termes de la suite.
- Ecrire la définition d'une méthode qui calcule la racine carrée de a en s'arrêtant quand l'intervalle entre deux termes successifs de la suite est plus petit que un ε donné.
- Ecrire la définition d'une méthode qui calcule la racine carrée d'un nombre en s'arrêtant quand l'intervalle entre deux termes successifs de la suite est plus petit que 10^-n. On utilisera la classe BigDecimal.
La méthode de Halley pour calculer la racine carrée d'un nombre est la suivante :
```
  x₀ = a/2
  x_n+1 = (x_n×x_n×x_n+3×a×x_n)/(3×x_n×x_n+a)
```
La méthode de HouseHolder pour calculer la racine carrée d'un nombre est la suivante :
```
  x₀ = a/2
  x_n+1 = (3×x_n×x_n×x_n×x_n+6×a×x_n×x_n-a×a)/(8×x_n×x_n×x_n)
```
Ecrire la définition d'une méthode qui calcule la racine carrée d'un nombre en s'arrêtant quand l'intervalle entre deux termes successifs de la suite est plus petit que 10^-n. On utilisera la classe BigDecimal. Comparer les vitesses (nombre d'itérations nécessaires) des différentes méthodes.
Le coefficient binomial est défini par 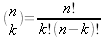ou par :

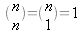
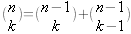pour 1<k<n. Ecrire la définition d'une méthode qui calcule le coefficient binomial pour deux entiers n et k pour chacune des définitions précédentes.
Un nombre de Fibonacci à l’ordre n est défini comme suit :
```
F₀=F₁=1
F_n= F_n-1 + F_n-2
```
Ecrire la définition d’une méthode récursive qui calcule le nombre de Fibonacci au rang n. Ecrire la définition d’une méthode itérative qui calcule le nombre de Fibonacci au rang n. Tester ces méthodes pour le calcul du nombre de Fibonacci aux rangs 40, 50, 60. Expliquer !
Un nombre de Padovan est défini par :
```
P₀=P₁= P₂=1
P_n+1= P_n-1 + P_n-2
```
Ecrire la définition d’une méthode qui calcule le nombre de Padovan au rang n.
Un nombre de Catalan est défini de la façon suivante :

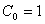
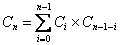
Ecrire la définition d’une méthode qui calcule le nombre de Catalan au rang n.
Ecrire la définition d’une méthode qui énumère la suite de Syracuse d’un nombre n.
- Si n est pair on le divise par 2 et on recommence
- Si n est impair on le multuplie par 3, on ajoute 1 et on recommence.
- On s’arrête lorsque n vaut 1.
Le code de Gray est un codage binaire des nombres entiers, tel que lorsqu'on passe d'un entier au suivant, un seul bit change dans la représentation de l'entier. Exemple :
```
 
 0
 1
 2
 3
 4
 5
 6
 7
 8
 
 
 0000
 0001
 0011
 0010
 0110
 0111
 0101
 0100
 1100
 
 
```
Un algorithme permettant de passer d'un nombre de Gray au suivant :
- si le nombre de 1 est pair, on inverse le dernier chiffre de la représentation.
- si le nombre de 1 est impair, on inverse le chiffre situé à gauche du 1 le plus à droite.
Ecrire la définition d'une méthode int graySuivant(int s) qui, à partir d'une représentation d'un nombre en code de Gray, calcule la représentation du nombre suivant.

Ecrire la définition d'une méthode int grayPrecedent(int s) qui, à partir d'une représentation d'un nombre en code de Gray, calcule la représentation du nombre précédent.

Ecrire la définition d'une méthode int int2gray(int n) qui, à partir d'un nombre n retourne sa représentation en code de Gray, sans calculer les représentations des nombres qui précèdent n. On pourra utiliser la formule codeGray(n) = n ^(n>>1).

Ecrire la définition d'une méthode int gray2int(int s) qui, à partir d'une représentation d'un nombre en code de Gray, calcule l'entier dont il est représentation.
Un nombre de Lychrel est un nombre naturel qui ne peut pas former de nombre palindrome lorsqu'il est soumis au processus itératif qui consiste à l'additionner au nombre formé de l'inversion de ses chiffres en base 10. Le nom Lychrel a été inventé par Wade VanLandingham : il s'agit d'une anagramme du nom de sa fiancée, Cheryl. Les nombres de Lychrel sont des nombres théoriques. On n'en connait aucun, bien que de nombreux nombres soient suspectés. Le plus petit nombre suspecté d'être de Lychrel est 196.
Définir une méthode qui programme le processus décrit, et qui s’arrête si le nombre donné en paramètre n’est pas un nombre de Lychrel.
Définir la méthode qui dit si deux nombres sont amicaux ou non. Deux nombres n et m sont amicaux si la somme des diviseurs de l’un est égale à la somme des diviseurs de l’autre et égale à n+m.

Définir la méthode qui dit si un nombre est parfait ou non. Un nombre est parfait s’il est égal à la somme de ses diviseurs stricts. 6 (1+2+3 est parfait).

Définir la méthode qui dit si un nombre est abondant ou non. Un nombre est abondant s’il est inférieur à la somme de ses diviseurs stricts.

Définir la méthode qui dit si un nombre est déficient ou non. Un nombre est déficient s’il est supérieur à la somme de ses diviseurs stricts.
L'algorithme d'Euclide permet de calculer le plus grand commun diviseur de deux entiers a et b.
- si b = 0 le pgcd est a
- si b != 0 le pgcd de a et b est le même que le pgcd de b et a%b
L'algorithme d'Euclide-Bezout permet de calculer le plus grand commun diviseur de deux entiers a et b, ainsi que deux entiers u et v tels que a×u + b×v = pgcd.
Ecrire la définition d'une méthode qui retourne vrai si l'entier en paramètre est un nombre premier et faux sinon. Le polynome x²+x+41 est réputé générer des nombre premiers. Définir une méthode qui trouve le premier nombre non premier généré par ce polynome.
L'algorithme d'Archimède pour calculer la valeur du nombre π consiste à calculer les périmètres de polygones réguliers inscrits et exinscrits dans un cercle de rayon 1.
Les demi-périmètres des polygones inscrits sont donnés par la suite :
```
    I₄=2×sqrt(2)
    I_2n=sqrt(I_n×E_2n)
```
Les demi-périmètres des polygones exinscrits sont donnés par la suite :
```
    E₄=4
    E_2n=2×I_n×E_n/(I_n+E_n)
```
On commence par les carrés inscrit et exinscrit, puis à chaque étape on double le nombre de cotés des polygones.
Une mauvaise méthode de calcul de π est une méthode monte-carlo. On tire au hasard un point dans le carré de coté 2. La probabilité pour que ce point se trouve à l'intérieur du cercle de rayon 1 inscrit dans ce carré est π/4. Ecrire la définition d'une méthode qui calcule π en tirant n points au hasard.
Le calcul de π peut se faire en utilisant la fraction continue suivante :

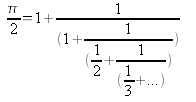
Ecrire la définition d'une méthode qui calcule π en utilisant la formule précédente au rang n.
Le calcul de π peut se faire en utilisant l'une des formules suivantes
- Leibniz
- Wallis
- Viète
- Brent et Salamin
- Plouffe
Pour chacune de ces formules, écrire la définition d'une méthode qui calcule π en utilisant la formule au rang n.
En 1974 Gosper a découvert la formule 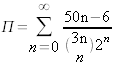. Ecrire la définition d'une méthode qui retourne la valeur de π en calculant la somme précédente au rang n.
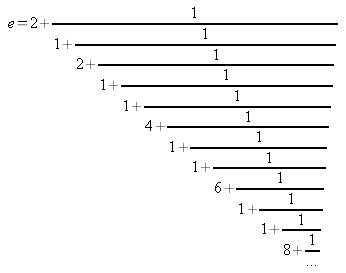
Le calcul de E peut se faire en utilisant l'une des formules suivantes :
- Jacob Bernoulli
- Euler
- Euler, fractions continues
Pour chacune de ces formules, écrire la définition d'une méthode qui calcule E en utilisant la formule au rang n.

haut de la page

0	1	2	3	4	5	6	7	8
0000	0001	0011	0010	0110	0111	0101	0100	1100