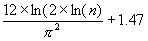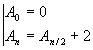dont la solution est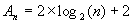 
précédent | suivant | table des matières
L’algorithme d’Euclide pour calculer le plus grand commun diviseur de deux nombres entiers est le suivant :
int pgcd ( int a, int b){
if(b==0) return a ;
else return pgcd(b, a%b);
}
L’analyse de l’algorithme n’est pas simple, en effet le nombre d’appels de la fonction va dépendre des valeurs de a et b. on peut cependant au moins affirmer que tous les deux appels le nombre a diminue au moins de moitié :
Si a>b, alors a%b<a/2. Deux cas se présentent :
Le nombre d’appels de la fonction est donc majoré par les termes de la récurrence :
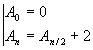dont la solution est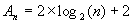
En fait , le cas le pire se produit lorsque a et b sont deux nombres de Fibonacci successifs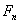 
et 
, et dans ce cas le nombre d’appels est exactement n. On en déduit que dans le pire des cas le nombre d’appels est au maximum de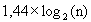 
.
L’évaluation en moyenne est malheureusement très compliquée, et nous donne un nombre d’appels 