précédent | suivant | table des matières

Complexité : Plus grande somme d’éléments consécutifs dans un tableau

(application)

Nous considérons un tableau d’entiers négatifs, positifs ou nuls. Nous nous proposons de calculer l’intervalle du tableau qui contient la somme la plus grande.

Programmation naïve

La programmation naïve consiste à énumérer tous les couples (i, j) qui délimitent une partie du tableau, à calculer la somme des éléments pour cette partie, et à calculer le maximum de toutes ces sommes.

public class Triplet {
    int somme; int d; int f;
    public Triplet ( int s, int d, int f){
      somme = s; 
      this.d = d;
      this.f = f;
}

int public Triplet plusGrandeSomme1(int t[]){
   int sommeMax = t[0], somme;
   int d = 0; int f = 0;
   for(int i = 0; i<t.length; ++i)
      for(int j = i; j<.length; ++j){
         somme = 0;
         for(int k = i; k <= j; ++k) 
            somme+=t[k];
            if(somme>sommeMax){
               sommeMax = somme;
               d = i; f = j;
            }
      }
      return new Triplet(sommeMax, d, f);
}

Calculons le nombre N de fois que l’instruction somme+=t[k] est effectuée : 

Or et il reste donc

Or (formule de Faulhaber voir démonstration en annexe) donc

Programmation améliorée

Dans l’algorithme précédent, les sommes partielles sont calculées plusieurs fois. On peut ne les calculer qu’une seule fois de la façon suivante : 

Triplet plusGrandeSomme2(int t[]){
   int sommeMax = t[0], somme;
   int d=0; int f=0;
   for(int i=0; i<t.length; ++i){
      somme = 0;
      for(int j=i; j<t.length; ++j){
         somme+=t[j];
         if(somme>sommeMax){
        	 sommeMax = somme; d = i; f = j;
         }
      }
   }
   return new Triplet(sommeMax, d, f);
}

Comptons le nombre N de fois que l’instruction somme+=t[j]; est exécutée : 

Diviser pour régner

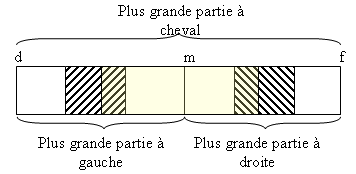
On peut utiliser la stratégie « diviser pour régner » pour concevoir un algorithme plus rapide. On découpe le tableau en deux parties de taille à peu près égales : la plus grande somme se trouve soit dans la partie de droite, soit dans la partie de gauche soit à cheval sur les deux parties. Dans ce cas elle est constituée d’une plus grande somme de la partie gauche se terminant à la fin de la partie gauche, et d’une plus grande somme de la partie droite commençant au début de la partie droite.

Triplet plusGrandeSomme3 (int t[], int d, int f){ 
   if(d==f) return new Triplet(t[d], d, f);
   int m = (d+f)/2;
   Triplet t1 = plusGrandeSomme3(t,  d, m );
   Triplet t2 = plusGrandeSomme3(t,  m+1, f ); 
   // calcul de la plus grande somme à cheval
   int s1=t[m], s1m=s1, dmg=m;
   for(int k = m-1; k>=d; --k){
      s1+=t[k]; if(s1>s1m){s1m=s1; dmg=k;}
   }
   int s2=t[m+1], s2m=s2, dmd=m+1;
   for(int k = m+2; k<=f; ++k){
       s2+=t[k]; 
       if(s2>s2m){s2m=s2; dmd=k;}
   }
   int sm3 = s1m+s2m;
   if(t1.somme>=t2.somme && t1.somme>=sm3)return new Triplet(t1.somme, t1.d, t1.f);
   if(t2.somme>=t1.somme && t2.somme>=sm3)return new Triplet(t2.somme, t2.d, t2.f);
   return new Triplet(sm3, dmg, dmd);
}

Le temps de calcul de la plus grande somme s’exprime par la récurrence :

Un temps proportionnel à n

On peut faire encore mieux en développant un algorithme qui prend un temps de calcul proportionnel à n : quand la somme devient négative, elle ne peut pas préfixer une plus grande somme, en effet il suffirait de l’ôter à la somme pour que cette somme devienne plus grande. Dans ce cas une plus grande somme suivante ne pourra commencer que en i+1.

Triplet plusGrandeSomme4(int t[]){
   int sommeMax = t[0], somme = 0;
   int d=0; int f=0;
   int  debutPGS = 0;
   for(int i=0; i<t.length; ++i){
      somme += t[i];
      if(somme>sommeMax){sommeMax = somme; d = debutPGS;  f = i;}
      if(somme<0){somme = 0; debutPGS = i+1;}
   }
   return new Triplet(sommeMax, d, f);
}

haut de la page