précédent | suivant | table des matières
Les cefficients du binôme sont définis par la récurrence :
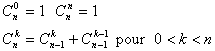
Programmation récursive
Une fonction récursive qui calcule ces coefficients est :
int coeffBin( int n, int k){
if(k==0 || k==n) return 1;
else return coeffBin(n-1, k) + coeffBin(n-1, k-1);
}
Le temps de calcul de cette fonction est proportionnel au nombre d’appels de la fonction : ce nombre d’appels est donné par la récurrence :
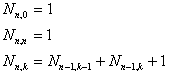On montre par récurrence que 
Les temps de calcul les plus longs sont donc quand k≈n/2
et donc dans ce cas : 
: on a alors : 
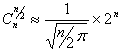( on utilise la formule de Stirling 
)
Triangle de pascal
Le coût de la programmation précédente est du au multiples calculs de la même valeur de 
. Pour minimiser ce coût on peut utiliser une technique de programmation dynamique qui consiste à stocker les valeurs intermédiaires pour ne pas les re-calculer : c’est le triangle de Pascal.
| 1 | ||||||||||||||||
| 1 | 1 | |||||||||||||||
| 1 | 2 | 1 | ||||||||||||||
| 1 | 3 | 3 | 1 | |||||||||||||
| 1 | 4 | 6 | 4 | 1 | ||||||||||||
| 1 | 5 | 10 | 10 | 5 | 1 | |||||||||||
| 1 | 6 | 15 | 20 | 15 | 6 | 1 | ||||||||||
| 1 | 7 | 21 | 35 | 35 | 21 | 7 | 1 | |||||||||
| 1 | 8 | 28 | 56 | 70 | 56 | 28 | 8 | 1 |
Pour calculer il suffit de remplir le tableau au rang n ; on a donc un coût proportionnel à 
.
long binome2( int n, int k){
long [][] t = new long[n+1][];
for(int i=0; i<=n; ++i){
t[i] = new long[i+1];
t[i][0] = 1;
for( int j = 1; j<i; ++j)
t[i][j] = t[i-1][j] + t[i-1][j-1];
t[i][i] = 1;
}
return t[n][k] ;
}
Exemple : la fonction caractéristique de la loi Γ tronquée est définie par :
pour 
et 0 sinon
Ecrire une programmation récursive, et donner une idée de solution utilisant la technique du triangle de Pascal.