précédent | suivant | table des matières

Complexité : Nombres de Fibonacci

(application)

Les nombres de Fibonacci sont définis par la récurrence :

• F₀ = 1
• F₁ = 1
• F_n = F_n-1+F_n-2 pour n≥2

Programmation récursive

long fibonR( int n ){
   if((n==0)||(n==1)) 
        return 1;
   else return fibonR(n-1)+fibonR(n-2);
}

Le nombre d'appels de la méthode fibonR générés par un appel de fibonR(n) est donné par la récurrence suivante 

• N₀ = 1
• N₁ = 1
• N_n = N_n-1+N_n-2+1 pour n≥2

On montre par récurrence que N_n=2×F_n-1.

La récurrence qui exprime le nombre de Fibonnacci au rang n se résout de la façon suivante :

Soient et les racines de l’équation sont et

On a

Or

On a alors

Donc et , le deuxième terme tend donc vers 0, donc le nombre d'appels récursifs a une croissance exponentielle !

Programmation itérative

long fibonI( int n ){
   long F0 = 1, F1 = 1, F = 1;
   for(int i = 2; i<= n; ++i){
      F = F0+F1;
      F0 = F1;
      F1 = F;
   }
   return F1;
}

Le temps de calcul est clairement de l'ordre de n.

Peut-on faire mieux ?

Soit 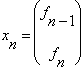alors on a : 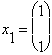 et .

On déduit que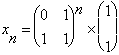

Nous nous proposons de calculer Mⁿ en faisant le moins possible de multiplications. L’algorithme classique effectue n multiplications. Pour en faire moins nous nous proposons de programmer l’algorithme suivant : 

• Mⁿ = (M*M)^n/2 si n est pair ( le signe / est le signe de la division entière )
• Mⁿ = M*(M*M)^n/2 si n est impair.

Supposons que n soit une puissance de 2. Le nombre de multiplications effectuées par cette méthode est donné par la récurrence : 

Soit

Dans ce cas le temps de calcul de est donc proportionnel à

public class Matrice {
   long A, B, C, D;
   Matrice(long a, long b, long c, long d){
      A=a; B=b; C=c; D=d;
   }
   public Matrice multiplie( Matrice m){
        long a, b, c, d;
         a = A*m.A + B*m.C;
         b = A*m.B + B*m.D;
         c = C*m.A + D*m.C;
         d = C*m.B + D*m.D;
         return new Matrice(a, b, c, d);
   }
}

Matrice xn( int n, Matrice m){
        if(n==0)      return new Matrice(1, 0, 0, 1);
        else if(n==1) return new Matrice(m.A, m.B, m.C, m.D);
        else {
           int n2 = n/2;
           Matrice res = xn(n2, m.multiplie(m));
           int nMod2 = n%2;
           if(nMod2!=0) res = m.multiplie(res);
           return res;
        }
  }

public  long fibonM(int n){
   Matrice m = new Matrice(0,1,1,1);
   return xn(n, m).D;
}

Exercice : A partir de quelle valeur de n les algorithmes précédents ont des temps de calcul sensiblement différents.

haut de la page