Précédent / Suivant / Table des matières

 

 

Problème : Coloration des sommets d’un graphe simple

Partie A : Préliminaires

1) (D’après « fête de la science  2002 »)

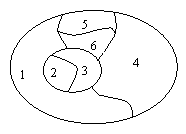
Combien faut-il de couleurs différentes au minimum pour colorier la carte suivante, qui comporte six zones, sans que deux zones limitrophes ne soient de la même couleur ?

 

 

2) Un concours comporte six épreuves A, B, C, D, E et F. Les candidats doivent choisir un ensemble d’épreuves parmi les suivants : {A, D, E} ; {C, F} ; {B, C} ; {B, E}. Chaque épreuve nécessite une demi-journée.

Quel est le nombre minimal de demi-journées nécessaires pour organiser le concours ?

Partie B : Stabilité et transversalité

Soit G=(S,A) un graphe simple d’ordre n. Un sous-ensemble XS est stable si deux sommets quelconques de X ne sont jamais adjacents. Un sous-ensemble TS est transversal si toute arête de A possède au moins une extrémité dans T.
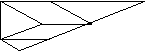
1) Donner un sous-ensemble stable formé de trois sommets et un sous-ensemble transversal formé de cinq sommets du graphe suivant :

 

 

 

 

 

 

2) Montrer que le complémentaire de tout sous-ensemble stable est transversal et réciproquement.
3) Soit G=(S,A) un graphe simple biparti. On désigne par S₁ et S₂ les sous-ensembles de sommets formant la bipartition. S₁ et S₂ sont-ils stables ? transversaux ? (Justifier votre réponse).
4) Notons Σ la famille des sous-ensembles stables de S et Φ celle des sous-ensembles transversaux de S. On appelle nombre de stabilité de S le nombre  où |X| est le nombre d’éléments de X. On appelle nombre de transversalité de S le nombre  où |T| est le nombre d’éléments de T.
Montrer que α(G)+τ(G)=n.

Partie C : Nombre chromatique

Colorer les sommets d’un graphe simple G=(S,A) consiste à leurs associer des couleurs (ou tout autre identificateur : numéro, nom …) de telle sorte que deux sommets adjacents n’aient pas la même couleur (le même numéro, le même nom …). Si k couleurs (numéros, noms …) sont utilisés on parle de k-coloration. On appelle nombre chromatique de G et on note γ(G) la plus petite valeur de k pour laquelle existe une k-coloration des sommets.
1) Donner une 3-coloration du graphe précédent.
2) Montrer qu’une k-coloration des sommets de G est équivalente à une partition de S en k sous-ensembles stables.
3) Quel est le nombre chromatique d’un graphe biparti ? D’un arbre ? D’un cycle élémentaire ?

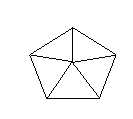
4) Donner le nombre chromatique du graphe suivant :

5) Montrer que g(G) ≤ 1+Δ(G) où  Δ(G) =Max{d(s_i) tq s_iS}. Appliquer au graphe précédent.
6) Montrer que γ(G) ≥ n/α(G).
7) Montrer γ(G) + α(G) ≤ n+1.

Partie D : Algorithme de Welsh & Powell

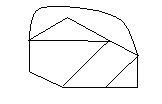
1) Colorer par l’algorithme de Welsh & Powell le graphe suivant :

2) Ecrire, dans votre langage favori, un programme de coloration des sommets d’un graphe simple.