Précédent / Suivant / Table des matières

 

 

Problème :

Partie A : Arbres couvrants

Définition : Soit G=(S,A) un graphe simple connexe d’ordre n et de taille p. On appelle arbre couvrant de G tout graphe partiel de G qui est un arbre. On note T=(S,B) cet arbre. Les arêtes de G qui ne sont pas dans T (dans B) sont appelées cordes (appellation abusive).
Théorème : (admis) Un graphe simple est connexe si et seulement si il admet un arbre couvrant.

1) Donner quelques arbres couvrants et le nombre de cordes pour chacun des graphes suivants :

 

2) Montrer que G contient p-n+1 cordes.
3) Montrer que pour tout arbre couvrant T=(S,B) de G, B contient toutes les arêtes pendantes de G.

4) Soit T=(S,B) un arbre couvrant de G. Si a=ss’ est une corde de G et a’=xy est une arêtes de la chaîne [s…s’] dans T, montrer que T’=(S,B’) avec B’=(B{a})\{a’} est un arbre couvrant de G.
5) Montrer que chaque arête de G appartient à au moins un arbre couvrant de G.

 

Partie B : MST (minimum spanning tree)

Définition : Le graphe G=(S,A) est dit pondéré s’il est muni d’une fonction π : A → R qui à toute arête a de A associe un nombre réel π(a) appelé poids de a.
Si T=(S,B) est un arbre couvrant de G alors, par définition, le poids de T .
Un arbre couvrant de poids minimum est un arbre couvrant T_M=(S,B_M) tel que
π( T_M)=Min{ π(T) , T arbre couvrant de G  }
Théorème : (admis) Tout graphe simple connexe admet un arbre couvrant de poids minimum. Si π est injective alors cet arbre est unique.

Algorithme de Kruskal :
(a) : Trier (et numéroter) les arêtes de G par ordre croissant de leur poids : π(a₁)≤ π(a₂)≤…≤π(a_p)
(b) : Lire la liste des arêtes triées. Au début B_M={a₁}. A l’étape k : lire l’arête a_k. Si a_k ne forme pas de cycle avec les arêtes de B_M alors ajouter cette arête à B_M (B_M= B_M { a_k }). Passer à l’arête suivante jusqu’à totaliser n-1 arêtes dans B_M.
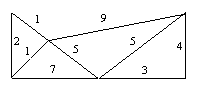
1) Appliquer l’algorithme de Kruskal en détaillant toutes les étapes au graphe suivant :

2) Quelle est le principe de base de cet algorithme ? Commenter.
3) Justifier que cet algorithme construit un arbre couvrant de poids minimum de G. Qu’obtient-on avec cet algorithme si à l’étape (a) on trie les arêtes de G par ordre décroissant ?
4) (travail personnel) Etudier l’algorithme de Prim et comparer.

5) (travail personnel) Ecrire, dans votre langage favori, un programme réalisant l’algorithme de Kruskal.

 

 

Partie C : Application

Le correspondant local d’une société qui organise des voyages dans les Alpes doit déterminer l’itinéraire reliant chaque paire d’un ensemble de lieux donnés, sous l’unique contrainte suivante : éviter les cols dont l’altitude est trop élevée (en raison de l’âge des participants).
1) Connaissant l’ensemble des lieux concernés et l’altitude maximale du tronçon reliant chaque paire de lieux voisins, modéliser la tâche du correspondant sous la forme d’un problème de graphe. Justifier l’algorithme utilisé.
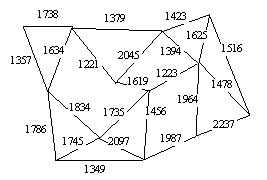
2) Résoudre le cas particulier donné par le réseau suivant. Les différents lieux sont représentés par les sommets du graphe. Deux lieux voisins sont reliés par une arête dont le poids est égal à l’altitude maximale du tronçon en question.