Précédent / Suivant / Table des matières

Problème :

Partie A : Préliminaire

1) On considère le plan d’une maison de cinq pièces A, B, C, D et E. On désigne l’extérieur par X. La communication entre les pièces et avec l’extérieur se fait par l’intermédiaire des portes. Vous êtes quelque part (à l’intérieur ou à l’extérieur). Vous est-il possible de traverser toutes les portes une et une seule fois ?

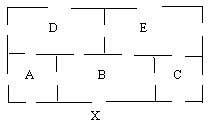
2) Peut-on aligner toutes les pièces d’un jeu de domino selon la règle habituelle du jeu de domino ? (Voir TD7 Exercice I)

Partie B :

Algorithme de Fleury :
(a) : Choisir un sommet s (respectivement un sommet impair s) et une arête incidente à s.
(b) : Choisir successivement des arêtes adjacentes de façon qu’à étapes, le graphe simple obtenu en effaçant l’arête choisie (et éventuellement un sommet autre que s devenu isolé) soit connexe.
1) Appliquer l’algorithme de Kruskal en détaillant toutes les étapes aux graphes suivants :

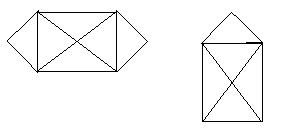
2) Quelle est le principe de base de cet algorithme ? Commenter.
Partie C : Graphes eulériens

Définition : Un cycle eulérien (respectivement une chaîne eulérienne) d’un graphe simple G=(S,A) est un cycle (respectivement une chaîne) contenant chaque arête de G une et une seule fois.
Définition : Un graphe simple est dit eulérien (respectivement semi-eulérien) s’il possède un cycle eulérien (respectivement une chaîne eulérienne).
1) a) Donner un graphe eulérien
     b) Donner un graphe semi-eulérien
     c) Donner un graphe ni eulérien ni semi-eulérien
2) Théorème d’Euler :
     a) Montrer que si G est un graphe simple eulérien alors il est connexe et tous ses sommets sont pairs.
     b) Montrer que si tous les sommets d’un graphe simple connexe G sont pairs alors il est eulérien.
     c) Montrer qu’un graphe simple connexe G est semi-eulérien si et seulement si il admet zéro ou deux sommets impairs.