Précédent / Suivant / Table des matières

 

 

Problème :

Le concept de graphe équilibré a été introduit par le psychologue Heider pour étudier les tensions pouvant surgir au sein d’un groupe de personnes liées par une relation (groupe de travail, parti politique, équipe …). Pour illustrer une telle situation on peut considérer un groupe de personnes dans lequel deux individus ont soit une relation favorable soit défavorable soit neutre. Par relation favorable on entend, par exemple, « les deux personnes peuvent travailler  ensemble », ou « les deux personnes partagent le même avis » etc. Par relation défavorable on entend, par exemple, « les deux personnes ne peuvent pas travailler  ensemble », ou « les deux personnes ne partagent pas le même avis » etc. En l’absence des deux cas « favorable » et « défavorable » la relation est considérée comme neutre. Cartwrigh et Harary ont contribué à la formalisation et à l’étude mathématique de telles situations.

L’objet de ce problème est de modéliser ce genre de situations et de répondre à un certain nombre de questions. (Interprétation et éventuellement aide à l’organisation des groupes).

 

On appelle graphe signé un graphe simple G=(S,A)  dont chaque arête est munie soit d’un signe «+» traduisant une relation favorable entre les deux sommets de cette arête soit d’un signe «-» traduisant une relation défavorable. L’absence d’arête entre deux sommets traduit la neutralité.
Une chaîne est dite positive si elle comporte un nombre pair d’arêtes négatives (signées négativement), elle est dite négative dans le cas contraire.

Exemple :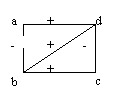

 (a,d) ; (b,d) ; (b,c)  sont trois couples de sommets en relation favorable
(a,b) et (c,d)  sont deux couples de sommets en relation défavorable
(a,c)  est un couple neutre
La chaîne adbc est positive, la chaîne adbcd est négative
Le cycle adba est négatif, Le cycle adcba est positif.

 

On dit qu’un graphe signé est équilibré si tous ses cycles élémentaires sont positifs.

1) a) Donner, à un isomorphisme près, tous les graphes complets signés à trois sommets. Indiquer les équilibrés.
     b) En analysant ces graphes à trois sommets, donner une interprétation, en terme de relation entre individus et effet sur le groupe, de la définition d’un graphe équilibré.

 

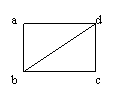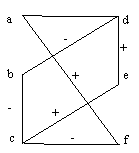
2) Signer par des «+» et des «-» le graphe ci-contre de telle manière à avoir trois graphes équilibrés et trois graphes qui ne le sont pas. Vérifier « intuitivement » que votre interprétation d’un graphe équilibré et « raisonnable ».

 

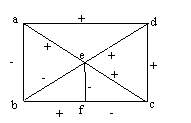
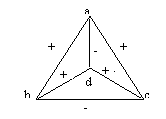3) Indiquer les graphes équilibrés parmi les suivants et retracer les en mettant en évidence une partition de l’ensemble des sommets S en deux sous-ensembles S₁ et S₂ tels que toute arête positive a ses deux sommets dans le même sous-ensemble et  toute arête négative a un de ses sommets dans un sous-ensemble et l’autre dans l’autre sous-ensemble.

 

 

 

 

 

 

4) On se propose de montrer que pour un graphe équilibré les quatre propositions suivantes sont équivalentes :

     (i)   Le graphe est équilibré

     (ii)  Tous les cycles sont positifs

     (iii) Deux chaînes ayant les mêmes extrémités sont de même signe

     (iv) Il existe une partition de l’ensemble des sommets S en deux sous-ensembles S₁ et S₂ tels que toute arête positive a ses deux sommets dans le même sous-ensemble et  toute arête négative a un de ses sommets dans un sous-ensemble et l’autre dans l’autre sous-ensemble.

     a) Montrer que (i)  (ii). Indication : Par l’absurde en considérant le plus court des cycles négatifs.
     b) Montrer que (ii)  (iii).
     c) Montrer que (iii)  (iv). Indication : On considère l’ensemble S₁ formé de la manière suivante : On place un sommet quelconque dans  S₁. Supposons avoir placé n sommets dans S₁, un autre sommet s sera placé dans S₁ s’il n’existe aucune chaîne négative ne le joignant à aucun des n sommets placés dans S₁. Le reste des sommets constituent S₂.
     d) Montrer que (iv)  (i).

5) Quelles applications peut-on envisager de l’équivalence : (i)  (iv) ?

 

 

6) Ecrire un programme réalisant cette partition. (Dans un langage de votre choix).