La récurrence qui donne la complexité en nombre de comparaisons du tri rapide, si la partition constitue deux parties de tailles égales, c'est à dire dans le meilleur des cas, est donc :
précédent | suivant | table des matières
Dans ce paragraphe nous supposerons que le choix du pivot se porte sur un quelconque des élément du morceau de tableau à partitionner. Alors la procédure de partition a clairement une complexité en nombre de comparaisons ∈ Θ(n) ;
La récurrence qui donne la complexité en nombre de comparaisons du tri rapide, si la partition constitue deux parties de tailles égales, c'est à dire dans le meilleur des cas, est donc :
.
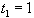
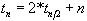
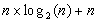La récurrence qui donne la complexité en nombre de comparaisons du tri rapide, dans le pire des cas, c'est à dire quand une des parties est vide et l'autre contient n-1 éléments est :
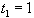
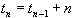
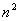
Le calcul de la complexité du tri rapide en moyenne est un peu plus compliqué. Supposons que le choix du pivot se porte de façon aléatoire sur chacun des éléments du tableau de taille n ; alors le coût moyen en nombre de comparaisons Cn est :
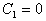
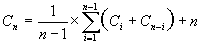
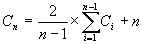
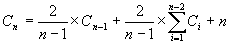
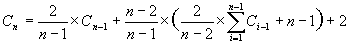le terme entre parenthèses est exactement Cn-1, donc :
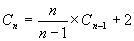
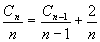
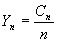,la récurrence s'écrit alors :
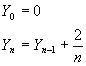
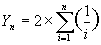
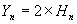Hn est le nombre harmonique au rang n.
Et donc en revenant à la récurrence Cn :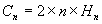 
Pour n grand, la formule d'Euler donne une relation entre le nombre harmonique de rang n et le logarithme de n :
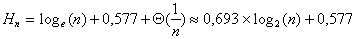
Il vient donc pour Cn :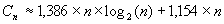 
donc la complexité moyenne du tri rapide appartient à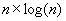 
.
La complexité spatiale, si les parties constituées par la partition sont de tailles à peu près égales,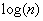 
et peut aller jusqu'à n lorsque la partition crée une des deux parties de taille 1. En revanche, si on prend soin de toujours faire le premier appel récursif sur la plus petite partie obtenue à la partition, alors la complexité spatiale est dans 
.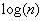