
les parties grisées peuvent être vides. Quand les parties grisées sont vides ( à l’initialisation ) la présence du pivot dans le tableau interdit les dépassements de bornes.
précédent | suivant | table des matières
Inventé par Hoare en 1961, ce tri s'appelle aussi parfois tri par segmentation, ou quicksort.
Le principe du tri est de créer une partition de l'ensemble E de départ en deux sous-ensembles E1 et E2 telle que les deux sous-ensembles une fois triés n'ont plus besoin d'être fusionnés, car la fusion ne serait qu'une mise bout à bout des deux sous ensembles E1 et E2.
Le principe de la partition est donc de choisir un élément pivot puis de ranger tous les éléments inférieurs ou égaux au pivot entre les indices d et i_pivot, et tous les éléments supérieurs ou égaux au pivot entre les indices i_pivot et f. La complexité temporelle du tri var dépendre de la qualité de la partition : si les deux parties créées sont de tailles égales la complexité sera dans l'ordre de n*log2(n), en revanche si une partie a une taille 1 et l'autre une taille n-1, la complexité sera dans l'ordre de n².
Une première idée de partition :
int partition1(int t[], int deb, int fin){ // deb < fin-1
int pivot = t[deb];
int iPivot= deb;
int d = deb, f=fin;
--d;
while(true){
assert((d==deb-1 && f==fin && d < f ) ||( t[d]<=pivot && t[f]>=pivot));
// invariant 1
// arrêt sur rep[f]<=pivot donc au moins sur le pivot la première fois
// ou sur un élément de la partie des <=
do{--f;} while (t[f]>pivot);
assert((d==deb-1 ) || ( f>=d && t[d]<=pivot && t[f]<=pivot));
// invariant 2
// arrêt sur rep[d]>=pivot donc au moins sur le pivot la première fois
// ou sur un élément de la partie des >= ensuite
do{++d;} while (t[d]<pivot);
assert(( t[d]>=pivot && t[f]<=pivot));
// invariant 3
if(d>=f) break;
assert(d < f &&( t[d]>=pivot && t[f]<=pivot));
// echanger(t[d], t[f]);
int a = t[d]; t[d]= t[f]; t[f]=a;
assert(d < f &&( t[d]<=pivot && t[f]>=pivot));
}
// d>=f ...
// la deuxième partie contient toujours au moins un élément
// c'est le pivot
assert(d<=fin);
if(d==deb) iPivot = d+1;else iPivot = d;
return iPivot;
}
invariant 1 : (d==deb-1 && f==fin && d < f ) || ( t[d]<=pivot && t[f]>=pivot)
 |
les parties grisées peuvent être vides. Quand les parties grisées sont vides ( à l’initialisation ) la présence du pivot dans le tableau interdit les dépassements de bornes. |
invariant 2: (d==deb-1 ) || (f>=d && t[d]<=pivot && t[f]<=pivot)
| ou | 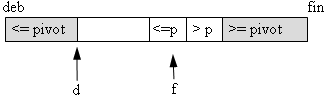 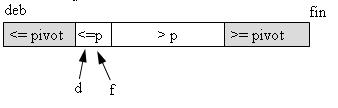
|
les parties grisées peuvent être vides. |
invariant 3: ( t[d]>=pivot && t[f]<=pivot)
ou ou encore s'il vient de se produire un échange de deux éléments consécutifs : |
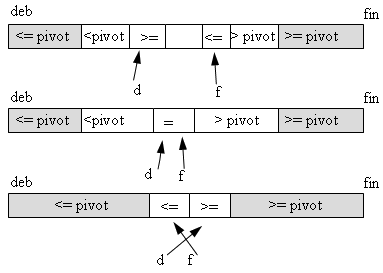 |
les parties grisées peuvent être vides. |
Cette partition crée une première partie à 1 élément lorsque le tableau initial est en ordre croissant … ce qui va impliquer une dégénérescence du tri rapide.
La qualité de la partition dépend du choix du pivot. L'idéal serait de choisir la médiane des n éléments de l'ensemble E de départ. Une solution simple et relativement efficace est de choisir la médiane parmi trois éléments, le premier, celui du milieu et le dernier.
int partition2(int t[], int deb, int fin ){
int iPivot;
int d=deb, f=fin;
int m = (d+f) / 2;
int pivot=t[d], b=t[m], c=t[f-1] ;
if( b>pivot){
int a = b; b = pivot; pivot = a;
} // b<=pivot
if( b>c){
int a = b; b = c; c = a;
}// b<=pivot && b<=c
if( pivot>c){
int a = pivot; pivot = c; c = a;
}// b<=pivot && b<=c && pivot<=c
--d;
while(d<f){
// invariant 1
// arrêt sur rep[f]<=pivot donc au moins sur le pivot la première fois
// ou sur un élément de la partie des <=
do{--f;} while (t[f]>pivot);
// invariant 2
// arrêt sur rep[d]>=pivot donc au moins sur le pivot la première fois
// ou sur un élément de la partie des >= ensuite
do{++d;} while (t[d]<pivot);
// invariant 3
if(d<f){
//echanger(t[d], t[f]);
in a = t[d]; t[d] = t[f]; t[f]=a;
}
}
// d>=f ...
// la deuxième partie contient toujours au moins un élément
// c'est le pivot
if(d==deb) iPivot = d+1;else iPivot = d;
return iPivot;
}
On peut optimiser l'espace occupé sur la pile en appelant d'abord récursivement le tri pour la partie la plus petite.
Remarque
Pour des tableaux de petite taille, le tri rapide devient mois efficace que le tri par insertion, et dans ce cas on termine donc par un tri par insertion. La condition d’arrêt dans l’algorithme du tri rapide devient :
if( d + TAILLELIMITE < f )
Et l’appel du tri rapide est suivi d’un appel du tri par insertion.