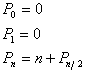précédent | suivant | table des matières

Tri par fusion pour les tableaux

Le tri par fusion pour les tableaux est défini par la fonction qui découpe le tableau initial en deux tableaux, et par la fonction de fusion.

Il y a plusieurs façon de découper le tableau initial T en deux tableaux T1 et T2 :

• la première moitié dans T1 et la deuxième dans T2
• les éléments de rang pair dans T1 et les élément de rang impair dans T2
• ...

On définit une méthode qui répartit les éléments alternativement sur deux tableaux :

void repartir( int t[], int t1[], int t2[]){
   for(int i = 0; i<n.length; ++i){
      t1[i/2] = t[i];
      ++i; if(i==n) break;
      t2[i/2] = t[i];
   }
}

Puis une fonction de fusion de deux tableaux ordonnés :

void fusionner(int t1[], int t2[], int t[]){
   int i1=0, i2=0, i=0;
   for( ; i1 < t1.length && i2 <t2.length; ++i )
      if(t1[i1]<t2[i2]){
         t[i]=t1[i1]; ++i1;
      }
      else {
         t[i]=t2[i2]; ++i2;
      }
   for( ; i1<t1.length; ++i, ++i1 ) t[i]=t1[i1];
   for( ; i2<t2.length; ++i, ++i2 ) t[i]=t2[i2];
}

Le tri par fusion s’écrit récursivement :

void triFusionR( int t[]){
   if(t.length<=1) return;
   else{
      int [] t1 = new int[(t.length+1)/2];
      int [] t2 = new int[t.length/2];
      repartir(t, t1, t2);
      triFusionR(t1);
      triFusionR(t2);
      fusionner(t1, t2, t);
   }
}

La programmation récursive est gourmande en place... Le besoin en place s’exprime par la récurrence :

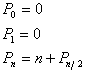dont la solution pour est 

On peut réduire le besoin en place en écrivant la fusion différemment :

int [] tAux;

void FusionSP(int t[], int d, int m, int f){
   // fusion de a [d, m[ et de a[m, f[
   int i, j, fAux=m-d, k;
   for(i=d, j=0; i<m; ++i, ++j)tAux[j]=t[i]; 

   i=m; j=0; k=d;
   for ( ; i<f && j<fAux; ++k)
      if( t[i]<taux[j]){ t[k]=t[i];    ++i;}
      else             { t[k]=tAux[j]; ++j;}
   for( ;i<f; ++i, ++k)    t[k]=t[i];
   for( ;j<fAux; ++j, ++k) t[k]=tAux[j];
}

void triFusionSP( int [] t, int d, int f){
   // tri par fusion de a entre d (inclus) et f (exclu)
   if(d>=f-1) return;
   else {
      int  m = (d+f)/2;
      triFusionSP(t, d, m);
      triFusionSP(t, m, f);
      FusionSP(t, d, m, f);
   }
}

void triFusionSP( int t[]){
   tAux = new int [(t.length+1)/2];
   triFusionSP( t, 0, t.length);
} 

La fusion sur place fonctionne de la façon suivante :

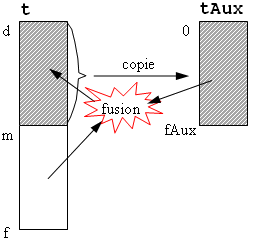
L’espace supplémentaire nécessaire n’est plus que de taille n/2.

haut de la page