précédent | suivant | table des matières
Supposons que le nombre n d'éléments de l'ensemble à trier soit tel que : 2p-1 < n < 2p
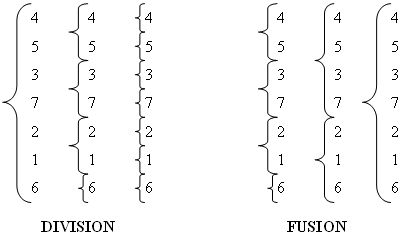
L'opération diviser de l'ensemble E en E1 et E2 consiste à ranger dans E1 les 2p-1 premiers éléments de E, et dans E2 les autres. L'opération recombiner est alors une fusion de deux ensembles.

Nous appelons monotonie une suite d'éléments ordonnés dans l'ordre croissant ( ou décroissant ).
La fusion fusionne des monotonies de longueur 1, 2 puis enfin 2p-1. La programmation itérative de l'algorithme est alors :
L'algorithme a une complexité en temps ![]()
La fonction suivante permet de répartir les élément du fichier fe alternativement sur fo1 et fo2.
public static int repartir(File fe, File fo1, File fo2, int l)throws IOException {
// distribue des monotonies de longueur l alternativement sur fo1, et fo2
// et retourne la longueur de fe
DataOutputStream o1 = new DataOutputStream(new FileOutputStream(fo1));
DataOutputStream o2 = new DataOutputStream(new FileOutputStream(fo2));
DataInputStream e = new DataInputStream(new FileInputStream(fe));
int n=0;
try {
while (true) {
for (int i = 0; i < l; ++i){
o1.writeInt(e.readInt());
++n;
}
for (int i = 0; i <l; ++i){
o2.writeInt(e.readInt());
++n;
}
}
} catch (EOFException e1) {
e.close();
o1.close();
o2.close();
return n;
}
}
La fonction suivante fusionne une monotonie de o1 avec une monotonie de o2. La longueur de chaque monotonie est l, sauf éventuellement pour la dernière monotonie qui peut être incomplète.
public static boolean fusionMonotonie(DataOutputStream e,
DataInputStream o1, DataInputStream o2, int l)
throws IOException{
// fusionne une monotonie de longueur l depuis o1 et o2 sur e
// éventuellement la dernière est plus courte.
// retourne true quand il n'y a a plus rien à fusionner :
// les deux monotonies à fusionner sont vides
int i = 0, j = 0, e1 = 0, e2 = 0;
boolean o1Fini = false, o2Fini = false;
i = 0;
try {
e1 = o1.readInt();++i;
} catch (EOFException e3) {
o1Fini = true;
}
j = 0;
try {
e2 = o2.readInt();++j;
} catch (EOFException e3) {
if(o1Fini) return true; // c'est fini !!!!
o2Fini = true;
}
while (!o1Fini && !o2Fini) {
if (e1 < e2) {
e.writeInt(e1);
if (i < l)
try {
e1 = o1.readInt();++i;
} catch (EOFException e3) {
o1Fini = true;
}
else o1Fini=true;
} else {
e.writeInt(e2);
if (j < l)
try {
e2 = o2.readInt();++j;
} catch (EOFException e3) {
o2Fini=true;
}
else o2Fini=true;
}
}
try {
while (!o1Fini) {
e.writeInt(e1);
if (i <l)
{e1 = o1.readInt();++i;}
else o1Fini=true;
}
} catch (EOFException e3) {}
try {
while (!o2Fini) {
e.writeInt(e2);
if (j <l)
{e2 = o2.readInt();++j;}
else o2Fini=true;
}
} catch (EOFException e3) {}
return false;
}
La fonction suivante fusionne pour tout i la monotonie de rang i de fo1 avec la monotonie de rang i de fo2, et distribue la monotonie obtenue alternativement sur fe1 et fe2.
public static void fusion(File fe1, File fe2, File fo1, File fo2, int l)
throws IOException {
DataOutputStream e1 = new DataOutputStream(new FileOutputStream(fe1));
DataOutputStream e2 = new DataOutputStream(new FileOutputStream(fe2));
DataInputStream o1 = new DataInputStream(new FileInputStream(fo1));
DataInputStream o2 = new DataInputStream(new FileInputStream(fo2));
while(true){
if(fusionMonotonie(e1, o1, o2, l)) break;
if(fusionMonotonie(e2, o1, o2, l)) break;
}
e1.close();
e2.close();
o1.close();
o2.close();
}
La fonction suivante effectue le tri du fichier nom en utilisant les différentes fonctions précédentes.
public static void triFusion(File fe)throws IOException{
int l=1;
File f1 = File.createTempFile("xxx", "tmp");
File f2 = File.createTempFile("xxx", "tmp");
File fe2 = File.createTempFile("xxx", "tmp");
int n = repartir(fe, f1, f2, l);
while(l<n){
fusion(fe, fe2, f1, f2, l);
l=l*2;
if(l>>=n) return; // le résultat est dans fe
fusion(f1, f2, fe, fe2, l);
l=l*2;
}
// le résultat est dans f1
fusion(fe, fe2, f1, f2, l);// fait une copie de f1 dans fe !
}
Remarques.
La rapidité du tri peut être augmentée, en augmentant le nombre de fichiers auxiliaires. On peut utiliser la mémoire centrale pour créer des monotonies initiales de longueur supérieure à 1 à l'aide d'un tri interne. Si le nombre de comparaisons reste dans le même ordre, le nombre de lectures-écritures sur fichier est considérablement réduit.
On peut utiliser les monotonies naturelles existant déjà dans le fichier initial. On montre que la longueur moyenne des monotonies est 2. On peut augmenter cette longueur à l'aide d'un tas.