précédent | suivant | table des matières
|
|
Les arbres rouge-noir sont des arbres binaires ordonnés (étendus) pour lesquels on a les propriétés suivantes :
1 Propriété.
La hauteur noire d’un nœud n notée hn(n) est le nombre de nœuds noirs dans un chemin du nœud à une de ses feuilles (le
nœud n n’est pas compris).
La hauteur noire d’un arbre rouge-noir est la hauteur noire de sa racine.
Un arbre rouge-noir contenant n nœuds internes a une
hauteur inférieure ou égale à 2×log2(n+1).
Montrons d’abord par induction sur la hauteur noire d’un nœud, que le nombre de nœuds internes du sous-arbre enraciné en x est au moins égal à 2hn(x) - 1.
![]()
![]()
![]()
2 Programmation.
Pour représenter un arbre binaire rouge-noir nous utilisonsune classe Noeud qui permet de représenter la couleur de l’arbre, et un attribut permettant de référencer son Noeud père. Pour les besoins de l’algorithme de suppression, chaque feuille au lieu d’avoir une référence null vers son fils gauche et son fils droit, aura une référence vers un nœud statique sentinelle de couleur noire.
static Noeud sentinelle;
static{
ArbreRougeNoir.sentinelle = new Noeud(null, Color.black, null, null);
}
class Noeud{
Color couleur;
Object info;
Noeud gauche, droit, parent;
Noeud(Object o){
couleur = Color.black;
info = o;
gauche = droit = parent = null;
}
Noeud(Object o, Color c, Noeud g, Noeud d, Noeud p){
couleur = c;
info = o;
gauche = g;
droit = d;
parent = p;
}
boolean isSentinelle(){
return this == ArbreRougeNoir.sentinelle;
}
2.1 Ajout.
L’ajout d’un nœud se fait de façon traditionnelle :
Noeud noeudAjoute;
public void ajout( Comparable o){
racine = ajout(o, racine, null);
}
private Noeud ajout( Comparable o, Noeud r, Noeud p){
// p est le parent de r
if (r.isSentinelle()) r = noeudAjoute = new Noeud(o, Color.red, r, r, p);
else
if(o.compareTo(r.info)<0) r.gauche = ajout(o, r.gauche, r);
else r.droit = ajout(o, r.droit, r);
return r;
}
Il suffit après l’insertion de réorganiser l’arbre, en partant du nouveau nœud ajouté, s’il ne possède plus une des propriétés précédentes :
Noeud noeudAjoute;
public void ajout( Comparable o){
racine = ajout(o, racine, null);
reOrganiser(noeudAjoute) ;
}
Un nœud ajouté est rouge. Si le nœud père est noir, l’arbre est toujours un arbre rouge-noir. En revanche si le nœud père du nœud ajouté est lui-même un nœud rouge, alors l’arbre a perdu sa propriété d’être un arbre rouge-noir.
Supposons que le parent du nœud n qui vient de briser la propriété de l’arbre d’être rouge-noir soit rouge et soit lui-même le descendant gauche de son père. Soit y le descendant droit du père du père de n. Dans ce cas il suffit de changer les couleurs du père de n de y et de leur père. Leur père devient rouge, et donc il faut réorganiser l’arbre à partir de ce nœud.
Le fait que n soit un fils droit ou un fils gauche de son père est indifférent.
Nous pouvons représenter cette configuration de la façon suivante :

En revanche si la couleur de y est noir, deux possibilités se présentent :

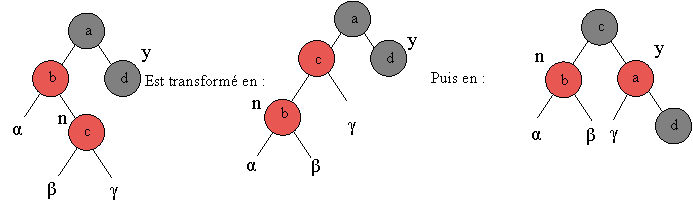
Si le père du nœud n est un fils droit de son propre père, les transformations sont complètement symétriques.
Nous voyons apparaître deux transformations d’arbres qui sont des rotations à gauche ou à droite :
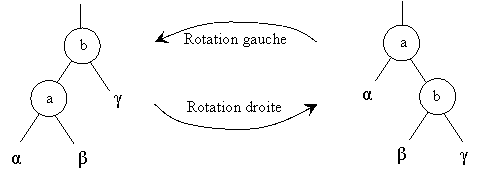
private void rotationGauche( Noeud n){
Noeud y = n.droit;
n.droit = y.gauche;
if(!y.gauche.isSentinelle())y.gauche.parent = n;// on ne change pas le parent de la sentinelle
y.parent = n.parent;
if (n.parent==null) racine = y;<
else
if( n.parent.gauche == n ) n.parent.gauche = y;
else n.parent.droit = y;
y.gauche = n;
n.parent = y;
}
private void rotationDroite( Noeud n){
Noeud y = n.gauche;
n.gauche = y.droit;
if(!y.droit.isSentinelle())y.droit.parent = n; // on ne change pas le parent de la sentinelle
y.parent = n.parent;
if (n.parent==null) racine = y;
else
if( n.parent.droit == n) n.parent.droit = y;
else n.parent.gauche = y;
y.droit = n;
n.parent = y;
}
La méthode de réorganisation de l’arbre est donc :
private void reOrganiser( Noeud n){
// re organisation de l'arbre, en remontant vers la racine
while(n != racine && n.parent.couleur == Color.red ){
if(n.parent == n.parent.parent.gauche){
Noeud y = n.parent.parent.droit;
if( y.couleur == Color.red ){
n.parent.couleur = Color.black;
y.couleur = Color.black;
n.parent.parent.couleur = Color.red;
n = n.parent.parent;
}else{
if(n == n.parent.droit){
n = n.parent;
rotationGauche(n);
}
n.parent.couleur = Color.black;
n.parent.parent.couleur = Color.red;
rotationDroite(n.parent.parent);
}
}else{
Noeud y = n.parent.parent.gauche;
if( y.couleur == Color.red ){
n.parent.couleur = Color.black;
y.couleur = Color.black;
n.parent.parent.couleur = Color.red;
n = n.parent.parent;
}else{
if(noeudAjoute == n.parent.gauche){
n = n.parent;
rotationDroite(n);
}
n.parent.couleur = Color.black;
n.parent.parent.couleur = Color.red;
rotationGauche(n.parent.parent);
}
}
}
racine.couleur = Color.black; // la racine est toujours noire
}
2.2 Suppression.
La suppression commence par une recherche classique du nœud à supprimer, puis enchaîne sur la réalisation de la suppression.
public void supprimer( Comparable o){
supprimer( racine, o );
}
private Noeud supprimer( Noeud r, Comparable o){
if(r.isSentinelle())return r; // Pas trouvé
if(o.compareTo(r.info)== 0) r = supprimer(r);
else
if(o.compareTo(r.info)<0) supprimer(r.gauche, o);
else supprimer(r.droit, o); return r;
}
La méthode suivante réalise la suppression du nœud, en le remplaçant par le plus petit élément de son sous-arbre droit, s’il a deux fils, et en le supprimant effectivement, s’il n’a qu’un seul fils.
private Noeud supprimer( Noeud z){
Noeud y, x;
if(z.gauche.isSentinelle() || z.droit.isSentinelle()) y = z;
else y = arbreSuccesseur(z);
if(!y.gauche.isSentinelle()) x = y.gauche;
else x = y.droit;
x.parent = y.parent;
if(y.parent== null) racine = x;
else
if( y == y.parent.gauche) y.parent.gauche = x;
else y.parent.droit = x;
if( y != z ) z.info = y.info;
// si le noeud supprimé est un noeud rouge, il n’y a rien à
// faire, l’arbre conserve ses propriétés
// en revanche si le nœud supprimé est noir,
// il faut reorganiser l’arbre
if ( y.couleur == Color.black) reOrganiserSuppression( x );
return y;
}
private Noeud arbreSuccesseur(Noeud x){
// le noeud successseur de x dans l'arbre,
// sentinelle si c'est le plus grand
if( !x.droit.isSentinelle()) return arbreMinimum(x.droit);
Noeud y = x.parent;
while(!y.isSentinelle() && x == y.droit){ x = y; y = x.parent;}
return y;
}
private Noeud arbreMinimum(Noeud x){
while( !x.gauche.isSentinelle()) x = x.gauche;
return x;
}
private void reOrganiserSuppression( Noeud n){
// re organisation de l'arbre, en remontant vers la racine
while(n != racine && n.couleur == Color.black ){
if(n == n.parent.gauche){
Noeud y = n.parent.droit;
if(y.couleur == Color.red ){
y.couleur = Color.black;
n.parent.couleur = Color.red;
rotationGauche(n.parent);
y = n.parent.droit;
}
if(y.gauche.couleur == Color.black && y.droit.couleur == Color.black){
y.couleur = Color.red;
n = n.parent;
}else{
if( y.droit.couleur == Color.black){
y.gauche.couleur = Color.black;
y.couleur = Color.red;
rotationDroite(y);
y = n.parent.droit;
}
y.couleur = n.parent.couleur;
n.parent.couleur = Color.black;
y.droit.couleur = Color.black;
rotationGauche(n.parent);
break;
}
}else{
Noeud y = n.parent.gauche;
if( y.couleur == Color.red ){
y.couleur = Color.black;
n.parent.couleur = Color.red;
rotationDroite(n.parent);
y = n.parent.gauche;
}
if(y.droit.couleur == Color.black && y.gauche.couleur == Color.black){
y.couleur = Color.red;
n = n.parent;
}else{
if( y.gauche.couleur == Color.black){
y.droit.couleur = Color.black;
y.couleur = Color.red;
rotationGauche(y);
y = n.parent.gauche;
}
y.couleur = n.parent.couleur;
n.parent.couleur = Color.black;
y.gauche.couleur = Color.black;
rotationDroite(n.parent);
break;
}
}
}
n.couleur = Color.black;
}