précédent | suivant | table des matières

Arbres binaires équilibrés : arbre 2-3-4.

1 Définition.

Les arbres 2-3-4 sont des arbres tels que  

1. tous les nœuds ont 2, 3 ou 4 fils.
   
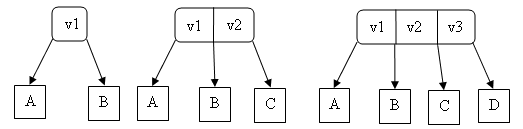
   Les sous-arbres A, B, C et D ont les propriétés suivantes : 
   • tous les nœuds du sous arbre A ont une valeur inférieure à v1.
   • tous les nœuds du sous arbre B ont une valeur supérieure ou égale à v1 et inférieure à v2, pour les nœuds 3 ou 4.
   • tous les nœuds du sous arbre Cont une valeur supérieure ou égale à v2 et inférieure à v3, pour les nœuds 4.
   • tous les nœuds du sous arbre D ont une valeur supérieure ou égale à v3.
2. tous les nœuds feuilles sont à la même profondeur.

Exemple d'arbre 2-3-4 obtenu par l'ajout des nombres de la séquence 10, 5, 8, 7, 15, 20, 12, 9, 13 :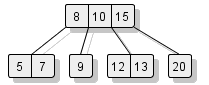 

2 Propriété.

La hauteur h de l'arbre 2-3-4 qui contient n valeurs est telle que :  log₄(n+1) ≤ h ≤ log₂(n+1).

En effet : 

• si tous les nœuds ont 2 fils, on a la hauteur maximum :  log₂(n+1)
• si tous les nœuds ont 4 fils, on a la hauteur minimum :  log₄(n+1)

3 Ajout.

L'insertion top-down se comporte de la façon suivante : 

Quand on descend dans l'arbre vers un nœud 4, celui-ci est éclaté avant d'y parvenir. Ainsi, ont est certain de ne jamais ajouter une nouvelle valeur dans un nœud 4.

1. Si le nœud 4 est la racine il est éclaté de la façon suivante :
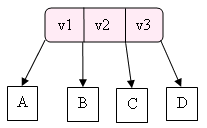   devient 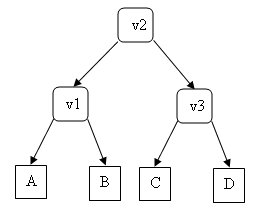C'est le cas où la hauteur de l'arbre augmente de 1.
2. Si le nœud 4 n'est pas la racine il est le fils d'un nœud 2 ou d'un nœud 3 (il ne peut pas être le fils d'un nœud 4 car celui-ci aura été éclaté lors de la descente) : 
   • il est le fils d'un nœud 2 : 
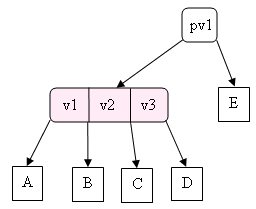     devient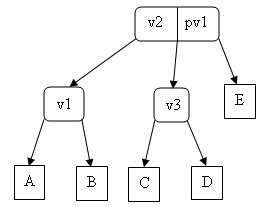
   • il est le fils d'un nœud 3 : 
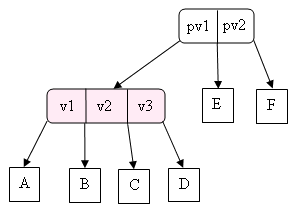     devient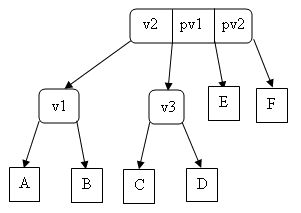
   Dans ces deux cas la hauteur de l'arbre n'est pas augmentée. Les transformations sont identiques si le nœud 4 à éclater est en position E ou F.

L'insertion conserve la propriété «toutes les feuilles sont à la même profondeur» : le seul moment où la hauteur de l'arbre augment, est lors de l"éclatement de la racine. Cet éclatement augmente les profondeurs de toutes les feuilles de 1.

4 Suppression.

Lors de la descente dans l'arbre, vers l'élément à supprimer, on fait les tranformations qu'il faut pour que le nœud où on arrive soit un nœud 3 ou un nœud 4 (sauf pour la racine).

1. J'ai un frère immédiat gauche ou droite qui est un nœud 3 ou un nœud 4 : 
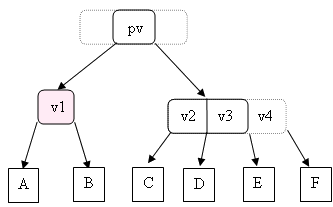   devient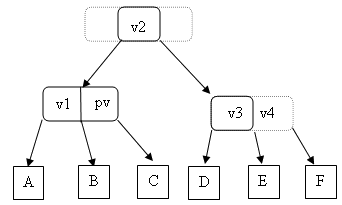
   Le principe est le même si c'est un frère à gauche.
2. Sinon, j'ai un frère immédiat gauche ou droite qui est un nœud 2 : 
   
   • Mon père est un nœud 2 : c'est la racine :
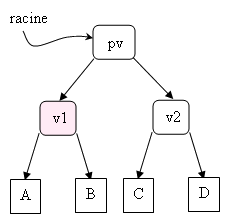     devient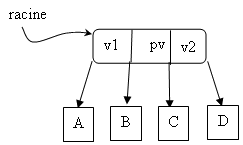
   • Mon père est un nœud 3 ou 4 : 
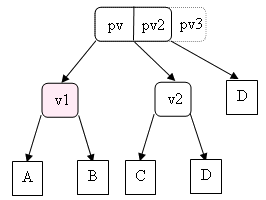     devient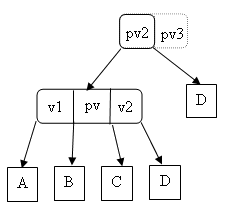

Quand on arrive sur un nœud qui contient l'élément à supprimer : 

• le nœud est une feuille, il suffit de supprimer l'élément.
• le nœud n'est pas une feuille :
  • les deux descendants droite et gauche ont 1 élément, on fusionne ces deux descendants et on supprime l'élément.
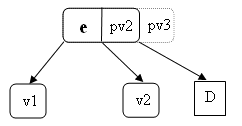    devient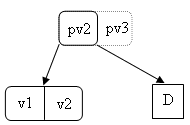
  • un des deux descendants a plus d'un élément, on remplace l'élément à supprimer par le succcesseur immédiat (ou le prédécesseur immédiat) de l'élément à supprimer.

haut de la page