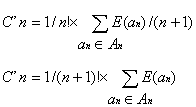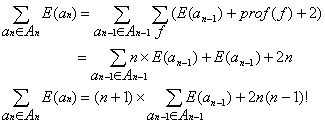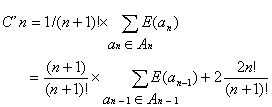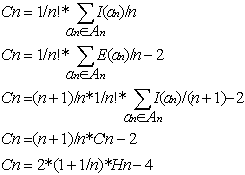précédent |
suivant |
table des matières
Arbre binaire, Arbre binaire ordonné.
1 Introduction.
Nous nous proposons d'implanter une classe ArbreBinaire permettant de stocker une
collections d'objets.
Les opérations que nous voulons pouvoir faire sur un objet
instance de la classe ArbreBinaire, sont les suivantes:
- Création.
- Nombre d'éléments de l'arbre binaire.
- Affichage de l'arbre binaire en infixé, préfixé, postfixé et indenté.
2 Noeud.
Chacun des élément de l'ArbreBinaire est représenté à l'aide
d'un objet instance de la classe Noeuddéfinie de la façon suivante:
class Noeud <E> implements Cloneable{
private E element;
private Noeud<E> gauche, droit;
public Noeud (){
element = null;
gauche = null;
droit = null;
}
public Noeud ( Object valeur, Noeud<E> g,
Noeud<E> droit){
element = valeur;
gauche = g;
droit = d;
}
public Object clone() throws CloneNotSupportedException{
Noeud<E> g = null;
if( gauche != null ) g = (Noeud<E>)gauche.clone();
Noeud<E> d = null;
if( droit != null ) d = (Noeud<E>)droit.clone();
return new Noeud<E>(element, g, d);
}
};
|
Un Noeud peut être représenté par:
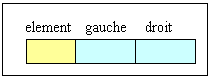
|
3 ArbreBinaire.
Nous nous intéresserons d’abord à la classe ArbreBinaire qui peut être définie de la
façon suivante:
public class ArbreBinaire<E> {
private Noeud<E> racine;
private void infixe(Noeud<E> r){...}
private void indente( Noeud<E> r, int n){...}
public ArbreBinaire(){...}
public int nombreElement(){...}
public int hauteur(){...}
public int nombreFeuilles(){...}
public void infixe (){...}
public void indente(){...}
public String parenthesee(){...}
public Object clone(){...}
}
Une instance de ArbreBinaire peut être représentée de la façon suivante:
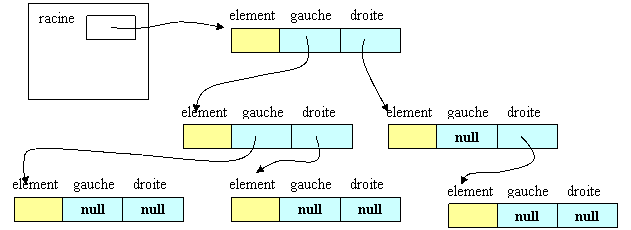
3.1 Affichage.
L'affichage en infixé d'un ArbreBinaire non vide
consiste en l'affichage en infixé du sous-arbre gauche, puis l'affichage de la
racine, puis l'affichage en infixé du sous-arbre droit.
void infixe(){
infixe (racine);
}
void infixe(Noeud<E> r){
if (r!=null) {
infixe(r.gauche);
System.out.print(r.element.toString()+" ");
infixe(r.droit);
}
}
L'affichage en indenté d'un ArbreBinaire non vide
consiste en l'affichage en indenté du sous-arbre gauche décalé vers la droite,
puis l'affichage de la racine, puis l'affichage en indenté du sous-arbre droit,
décalé vers la droite.
void indente(){
indente (racine, 0);
}
void (Noeud<E> r, int n){
if (r!=null){
indente(r.gauche, n+3);
for( int I = 0; i< n; ++i) System.out.print(" ");
System.out.print(r.element)
indente(r.droit, n+3);
}
}
3.21 nombre d’éléments, hauteur, nombre de feuilles.
int nombreElement(){
return nombreElement(racine);
}
int nombreElement(Noeud<E> r){
if (r==null)return 0;
else return nombreElement(r.gauche) + 1 + nombreElement(r.droite);
}
int hauteur(){
return hauteur(racine);
}
int hauteur(Noeud<E> r){
if (r==null) return 0;
else return max( hauteur(r.gauche), hauteur(r.droite)) + 1;
}
int nombreFeuilles(){
return nombreFeuilles(racine);
}
int nombreFeuilles(Noeud<E> r){
if (r==null)return 0;
else
if(r.gauche==null && r.droite==null) return 1;
else return nombreFeuilles(r.gauche) + nombreFeuilles(r.droite));
}
3.3 Forme parenthésée.
La forme parenthésée d’un arbre binaire est obtenue en
construisant une chaîne de caractère contenant: l’élément, puis entre
parenthèses et séparés par une virgule, les formes parenthésées de ses deux
fils. null est représenté par la chaîne de caractères vide.
String parenthesee(){
return parenthesee(racine);
}
String parenthesee(Noeud<E> r){
if (r==null) return "";
else return r.element.toString()+"("+ parenthesee(r.gauche)+", "+parenthesee(r.droit)+")";
}
<4 Arbre binaire ordonné.
Pour la suite, nous appellerons Arbre Binaire Ordonné un arbre binaire tel que l’attribut element e possède les propriétés
suivantes :
- e a une valeur supérieure aux valeurs des attributs element de tous les noeuds du sous-arbre gauche.
- e a une valeur inférieure aux valeurs des attributs element de tous les noeuds du sous-arbre droit.
Les objets rangés dans un arbre binaire ordonné devrons implémenter l’interface Comparable.
class ArbreBinaireOrdonne <E extends Comparable<E>> extends ArbreBinaire<E>{
public void ajout(E o){...}
public void suppression(E o){...}
public Noeud<E> chercher(E o){...}
private void ajout ( Noeud<E> r, E o){...}
private void suppression (Noeud<E> racine, E o){...}
private Noeud chercher(Noeud<E> r, E o){...}
private void supp (Noeud<E> r){...}
};
4.1 Ajout.
void ajout(E o){
racine = ajout(racine, o);
}
Noeud ajout ( Noeud<E> r, E o){
if(r==null)
return new Noeud<E> (o, null, null);
else
if (r.element.compareTo(o)<0) r.droit = ajout(r.droit, o);
else if (r.element.compareTo(o)>0) r.gauche = ajout(r.gauche, o);
return r;
}
4.2 Suppression.
void suppression(E o){
racine = suppression(racine, o);
}
Noeud suppression(Noeud<E> r, E o){
if (r==null) return r;// l’objet o n’est pas trouvé
else{
if (r.element.compareTo(o)==0) return supp(r);
else if(r.element.compareTo(o)>0) r.gauche = suppression(r.gauche, a);
else r.droite = suppression(r.droite, a);
return r;
}
}
La fonction supp est définie comme suit : Il faut distinguer 3 cas:
- Le champ gauche est null : r devient égal au champ droit.
- Le champ droit est null : r devient égal au champ gauche
- Les champs gauche et droit sont différents de null : on remplace la racine de l'arbre binaire par le plus grand élément du sous-arbre gauche.
Noeud<E> supp (Noeud<E> r){
if(r.gauche==null) return r = r.droite;
else
if(r.droite==null) return r = r.gauche;
else{
Noeud<E> r1 = r.gauche;
Noeud<E> pere = r;
while(r1.droite!=null) {
pere = r1;
r1 = r1.droite;
}
r.element = r1.element;
if(pere == r) pere.gauche = r1.gauche;
else pere.droite = r1.gauche;
return r;
}
}
4.3 Recherche.
La méthode de recherche associative dans un arbre binaire ordonné, si l'élément cherché n'est pas à la racine, effectue la recherche que
dans un des sous-arbres:
Noeud<E> chercher(Noeud<E> r, Comparable o){
if (r==null) return null;
else if (r.element.compareTo(o)==0) return r;
else
if(r.element.compareTo(o)>0) return chercher(r.gauche, e);
else return chercher(r.droite, e);
}
4.4 Clonage.
Object clone() throws CloneNotSupportedException{
ArbreBinaireOrdonne abo = new ArbreBinaireOrdonne<E> ();
if(racine != null) abo.racine = (Noeud<E>) (racine.clone());
return abo;
}
5 Evaluation.
Nous nous proposons de calculer C'n coût moyen de la recherche d'un Noeud
non présent dans un arbre binaire ordonné de n éléments.
Cette moyenne nous la calculons sur l'ensemble des n! arbres binaires obtenus à partir des n!
permutations de n attributs element, ces permutations étant équiprobables.
Soit E(an) le cheminement externe d'un arbre binaire de n éléments, et An l'ensemble des arbres
binaires ordonnés de n éléments. Le coût C'n peut alors s'écrire de la façon suivante :
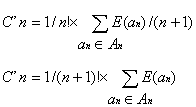
Or pour obtenir un arbre binaire an de n éléments, une feuille (nœud étendu)
est remplacée par un noeud interne, et il y a création de 2 nœuds étendus Nous pouvons donc écrire:
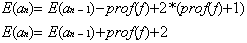
De plus pour un arbre binaire an :
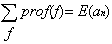
et le nombre de feuilles (nœud étendu) est égal à n+1
Nous pouvons alors écrire :
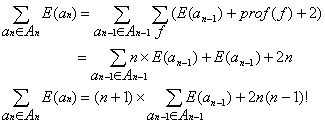
Nous obtenons enfin la récurrence cherchée sur C'n:
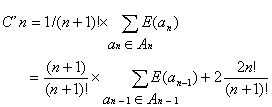
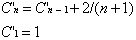
La solution de cette récurrence est :
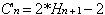
Le calcul de Cn coût moyen de la recherche d'un Noeud présent dans l’arbre binaire se déduit facilement. En effet :
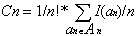
Or :
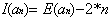
Donc :
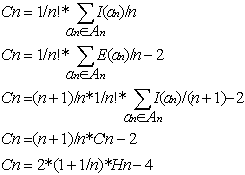
Or pour n suffisamment grand nous avons :
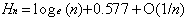
Donc :
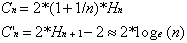
haut de la page