- La racine de l'arbre est A.
- m=4
- r1=B, r2=C, r3=D, r4=E.
- N1=(B,H) N2=(C,F,G) N3=(D,I,J,K) N4=(E).
précédent | suivant | table des matières
|
|
1 Définitions.
Graphe orienté.
Un graphe orienté est défini par le couple (N, A) :
Un graphe orienté peut être considéré comme une représentation d'une relation binaire R sur l'ensemble N :
Soient a et b appartenant à N alors : aRb ⇔ ∃x ∈ A et x = ab
Graphe non orienté
Un graphe est non orienté, si on ne distingue pas le sommet de départ et le sommet d'arrivée.
Successeur, prédécesseur
La relation successeur est une application de N dans l'ensemble ℘(N), ensembles des parties de N, qui à tout n appartenant à N associe l'ensembles des a appartenant à N tels que na appartient à A.
La relation prédécesseur est une application de N dans l'ensemble ℘(N), ensemble des parties de N, qui à tout n appartenant à N associe l'ensembles des a appartenant à N tels que da appartient à A.
Chaîne, cycle, chemin, circuit
Une chaîne est une séquence d'arêtes {a1, ... ak} telle que pour tout i de 1 à k-1 les arêtes ai et ai+1 ont une extrémité commune. Un cycle est une chaîne telle que a1 et akont une extrémité commune.
Un chemin est une séquence d'arêtes {a1, ... ak} telle que pour tout i de 1 à k-1 les arêtes ai et ai+1 ont une extrémité commune, cette extrémité étant de type arrivée pour ai et départ pour ai+1. Un circuit est un chemin tel que a1 et ak ont une extrémité commune, cette extrémité étant de type arrivée pour ak et départ pour a
La longueur du chemin, chaîne, circuit ou cycle est le nombre d'arêtes formant ce chemin, chaîne, circuit ou cycle.
Racine
Un graphe admet une racine r si pour tout n appartenant à N il existe un chemin de r à n. Un graphe sans circuit qui admet une racine, en admet une seule.
Connexe
Un graphe est connexe si et seulement si ∀( n1, n2) ∈N×N, ∃ une chaîne de n1 à n2.
Arbre
Un arbre est un graphe connexe sans cycle et muni d'une racine.
Une structure d'arbre induit une partition sur l'ensemble des noeuds de l'arbre :
Cette définition peut s'écrire de la façon suivante :
A→∅
A→ <r , A1, A2, ... An>
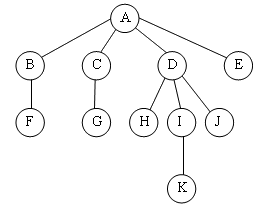
exemple :
N=(A,B,C,D,E,F,G,H,I,J,K).
|
 |
Cet arbre peut être représenté sous forme indentée :
A
B
F
C
G
D
I
K
J
E
Il peut être aussi représenté sous forme parenthésée : (A (B (F), C( G ), D(I(K), J),E ))
Ascendance, Descendance
Soit n1,n2, ... nk k noeuds d'un arbre tels que : ∀i, 1 ≤i ≤k on a ni = prédécesseur(ni+1).
Une telle suite est appelée chemin entre le noeud n1 et le noeud nk. La longueur du chemin est égale au nombre d'arêtes, c'est à dire au nombre de noeuds - 1.
S'il existe un chemin du noeud a vers le noeud b on dit que a est un ascendant de b, ou que b est un descendant de a.
Hauteur, profondeur, niveau
La hauteur
d'un noeud est la longueur du plus long chemin de
ce noeud aux
feuilles qui en dépendent plus 1 : c'est le nombre de
nœuds du chemin.
La hauteur
d'un arbre est la hauteur de sa racine. L'arbre vide a une
hauteur
0, et l'arbre réduit à une racine a une hauteur 1.
La profondeur
d'un noeud dans un arbre est le nombre de noeuds
du chemin
qui va de la racine à ce noeud. La racine d'un arbre est
à une profondeur 1,
et la profondeur d'un noeud est égale à la
profondeur de son prédécesseur
plus 1. Si un noeud est à une profondeur p, tous ses
successeurs sont à une
profondeur p+1.
Tous les noeuds d'un arbre de même profondeur sont au même niveau.
Feuille, Noeud interne
Une feuille ou noeud terminal est un noeud qui n'a pas de successeur.
Tout noeud d'un arbre qui n'est pas une feuille est un noeud interne.
Forêt
Nous appellerons forêt un ensemble ordonné d'arbres.
Remarque : les sous-arbres d'un noeud dans un arbre ordonné, forment une forêt.
Arbre n-aire
Un arbre est un arbre n-aire si tous les noeuds de l'arbre ont au plus n successeurs.
Arbre binaire
Un arbre est un arbre binaire, si tout noeud de l'arbre a 0, 1, ou 2 successeurs. Ses successeurs sont alors appelés respectivement successeur gauche et successeur droit. Lorsque tous les noeuds d'un arbre binaire ont deux ou zéro successeurs nous dirons que l'arbre binaire est homogène. Un arbre binaire est arbre binaire dégénéré si tous ses noeuds n'ont qu'un seul descendant.
Un arbre binaire complet est un arbre binaire tel que chaque niveau de l'arbre est complètement rempli. Un arbre binaire complet de hauteur h contient donc 2h-1 nœuds, et son nombre de feuilles est : Fh = 2h-1.
On commence par calculer le nombre de feuilles d'un arbre
binaire
complet. La démonstration se fait par récurrence :
Soit Nh = F1 + F2 + ...+ Fh = 1+2+ ...+2h-1= Σi=0 h-12i = 2h-1
Un arbre
binaire parfait est tel que tous les niveaux sauf
éventuellement
le dernier sont remplis, et dans ce cas les feuilles du dernier niveau
sont
groupées à gauche.
Un arbre binaire
parfaitement équilibré
est un arbre binaire complet dont
les noeuds de l'avant dernier niveau peuvent n'avoir qu'un seul
descendant.
Un arbre binaire est localement
complet si tous les noeuds qui
ne sont pas
des feuilles ont deux fils.
Un arbre binaire
étendu est un arbre binaire dans
lequel nous remplaçons
tout descendant vide par un noeud spécial noté  .
.
Exemple :
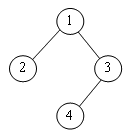 |
Est étendu en : | 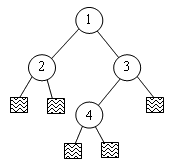 |
On démontre facilement par récurrence sur le nombre n de noeuds de l'arbre initial que le nombre C de noeuds étendus est tel que : C = n + 1
Le cheminement
interne
d'un arbre binaire est
la somme, pour tous les noeuds de l'arbre, des profondeurs des noeuds.
C'est
la somme des profondeurs de tous les noeuds de l'arbre. Dans l'exemple
précédent le cheminement interne est
égal à 8.
Le cheminement
externe d'un arbre binaire est la somme, pour
tous les
noeuds de l'arbre binaire étendu, des longueurs des chemins
de la racine à ce
noeud. C'est la somme des profondeurs des noeuds . Dans l'exemple
précédent
le cheminement externe est égal à 17.
Ces deux quantités sont liées respectivement au coût de la recherche avec succès et sans succès d'un noeud dans un arbre binaire. Le cheminement interne divisé par n (le nombre de recherches) est le coût moyen de recherche d'un noeud présent dans un arbre binaire ordonné. Le cheminement externe divisé par n est le coût moyen de recherche pour un noeud non présent dans un arbre binaire ordonné.
On démontre par récurrence sur le nombre de noeuds que si E est le cheminement externe et I le cheminement interne : E = I + 2×n + 1
 augmente de 1
également.
augmente de 1
également.2 Propriétés.
Propriété 0.Soit un arbre binaire de n noeuds et de f feuilles. On a : f≤(n+1) /2
Propriété 1.
Un arbre binaire ayant n noeuds a une hauteur h telle que : log2(n+1) ≤ h ≤ n
Propriété 2.
Tout arbre binaire ayant f feuilles a une hauteur supérieure ou égale à log2(f). La fonction logarithme est croissante donc log2(f) ≤ log2((n+1)/2)
soit 1+ log2(f) ≤ log2(n+1)
1 + log2(f) ≤ log2(n+1) = 1 + log2(n)
Propriété 3.
Le cheminement interne I d'un arbre binaire de n noeuds est : (n+1) × (log2(n+1) - 1) +1 ≤ I ≤ n(n-1)/2
3 Représentation des arbres N-aires.
Les arbres N-aires sont représentés en utilisant deux liens : un lien horizontal et un lien vertical.
Exemple : 
Un arbre N-aire est donc représenté comme un arbre binaire.
4 Représentation des arbres binaires.
4.1 Représentation contigüe.
Les noeuds de l'arbre sont rangés dans un tableau à une dimension ; les successeurs gauche et droit du noeud de l'arbre représenté à l'indice I dans le tableau, sont représentés respectivement dans les élément d'indice 2*I +1 et 2*(I + 1) , et la racine est à l’indice 0.
L'arbre :
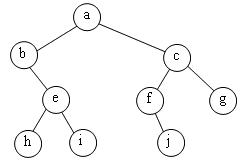
Est représenté
par :
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| a | b | c | e | f | g | h | i | j |
Un arbre binaire parfait a une représentation compacte sans trous dans le tableau:
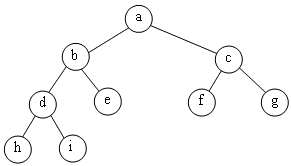
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| a | b | c | d | e | f | g | h | i |
4.2 Représentation chaînée.
Pour représenter les arbres de façon chaînée nous utilisons une classe Nœud qui contient 3 champs : un champ pour représenter l’information liée au nœud, et deux champs pointeurs vers les sous-arbres droit et gauche.