Précédent / Suivant / Table des matières

 

Exercice I :

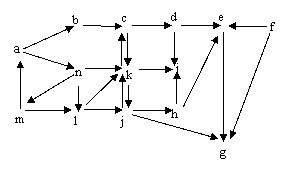
Dans le réseau de rues suivant les ronds représentent les carrefours et les flèches les sens de circulation.

1) Construire le graphe G=(S,A) dont les sommets sont les carrefours et dont les arcs sont définis par : a=(s,s’) est un arc si un automobiliste peut se rendre du carrefour s au carrefour s’ en respectant le sens de la circulation et sans passer par un carrefour intermédiaire.
2) Déterminer Γ⁺(e), Γ^-(e), d⁺(e) et d ^-(e).
3) Donner le sous-graphe engendré par S’=S\{ e }
4) Donner le graphe partiel engendré par A’=A\{(d,e)}
5) Existe-t-il une chaîne du sommet h au sommet l ? Existe-t-il un chemin du sommet h au sommet l ?
6) Donner trois chemins distincts joignant le sommet a au sommet e.
7) Donner un chemin élémentaire joignant le sommet a au sommet f.
8) Donner un chemin simple mais non élémentaire joignant le sommet a au sommet f.
9) Extraire un chemin élémentaire du chemin suivant iheabcjkjcdeabcjigf.
10) Soit X={a,d,e,h} déterminer ω⁺(X), ω^-(X), d⁺(X) et d ^-(X). Donner le cocycle engendré par X.
11) Donner la matrice d’adjacence M de G. En déduire les différents degrés et vérifier les théorèmes classiques.
12) Calculer (à l’aide d’un logiciel de calcul formel) M² et M³.
13) Donner la matrice d’incidence de G.
14) Le graphe G est-il connexe ? Est-il fortement connexe ?

 

Exercice II :

Soit G=(S,A) un graphe orienté avec S={s₁, s₂, s₃, …, s_n}. Pour tout couple (s_i,s_j) de S on pose :

On appelle piste un chemin de longueur minimale (on note π(s_i,s_j)).

Soit kN, à un sommet s on associe l’ensemble D_k(s)={s’S tel que d(s_i,s_j)=k}. On appelle descendants d’ordre k de s les éléments de D_k(s).
On considère la matrice D=(d_ij) dont les lignes et les colonnes sont indexées par S et définie par : d_ij = d(s_i,s_j). D est la matrice des distances de G.

Partie 1 :

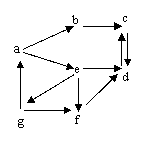
1) Donner la matrice d’adjacence M et la matrice des distances D du graphe ci-contre.

2) L’application d : S → R qui à (s_i,s_j) associe d(s_i,s_j) est-elle une distance (métrique) au sens topologique usuel ?
3) Soit M=(m_ij) la matrice d’adjacence de G et m_ij^(k) les coefficients de M^k .
On pose : E={k tel que 0< k <n et m_ij^(k) >0} pour i≠j.
Montrer que si E= alors d_ij = ∞ sinon d_ij =minE.

4) A l’aide de la matrice d’adjacence trouver la matrice des distances du graphe ci-contre :

 

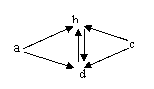
Partie 2 : Algorithme de Moore

Soit s un sommet de G. On considère la procédure d’étiquetage suivante :
Etape 0 : On donne l’étiquette 0 au sommet s
Etape 1 : On donne l’étiquette 1 à tous les successeurs du sommet étiqueté 0
Etape 2 : On donne l’étiquette 2 à tous les successeurs non étiquetés des sommets étiquetés 1