Précédent / Suivant / Table des matières

 

 

Exercice I :

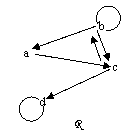Dans toute la suite E est un ensemble fini non vide ayant n éléments et R  est une relation binaire définie sur E. On désigne par p le nombre d’éléments (de couples) de R et par M sa matrice booléenne.
Pour les vérifications dans un cas particulier on utilisera l’ensemble E={a, b, c, d} et  la relation R  donnée par son diagramme sagittal (graphe) :

 

1) On représente R  par un tableau bidimensionnel T[1..n][1..n].
     a) Quel est l’occupation mémoire ?
     b) Quel est le nombre d’opérations élémentaires (addition et multiplication booléennes) doit-on effectuer pour calculer M² ?
2) On représente R  par sa table de successeurs. Pour cela on numérote les éléments de E de 1 à n et on se donne deux tableaux unidimensionnels T[1..n] et S[1..p] où les successeurs d’un sommet i sont donnés par les éléments : S[T[i]], … , S[T[i+1] -1]
     a) Quel est l’occupation mémoire ?
     b) Représenter la relation de l’exemple précédent.
3) On représente R  par deux tableaux unidimensionnels D[1..p] et F[1..p] où pour tout couple a_i=(x,y)R    D[i]=x et F[i]=y.
     a) Quel est l’occupation mémoire ?
     b) Représenter la relation de l’exemple précédent.
3) On représente R  par des listes chaînées : A chaque élément x_i on associe la liste de ses successeurs.
     a) Quel est l’occupation mémoire ?
     b) Représenter la relation de l’exemple précédent.

Exercice II :

Dans toute la suite E est un ensemble fini non vide ayant n éléments et R  est une relation binaire définie sur E. On désigne par M la matrice booléenne de R . Rappelons (Ex II TD3) que la fermeture transitive de R est donnée par
1) On considère la suite matricielle (S_k) définie par : S₁=M et S_k=M+M²+…+M^k  1≤k≤n
  a) Etablir une relation de récurrence entre S_k et S_k+1
  b) En déduire un algorithme pour calculer la matrice S de R ⁺.
  c) Pour k>1 évaluer le nombre d’opérations élémentaires (addition et multiplication booléennes) pour calculer S_k. Quelle est la complexité de cet algorithme ?

 

Application : Reprenons l’exercice I du TD II

E={a, b, c, d, e, f, g, h} désigne un ensemble d’émissions de télévision. Le père, la mère et le fils d’une même famille ont chacun classé ces émissions par ordre de préférence :
     père : a, b, c, d, e, f, g, h
     mère : a, c, f, b, d, e, g, h
     fils : a, b, c, e, f, d, h, g
On se propose d’étudier l’existence d’un ordre de préférence pour l’ensemble de la famille.
On dira que l’émission x est préférée à l’émission y si au moins une personne de la famille préfère x à y. Cette relation R n’est pas transitive (voir TD II exercice I). Convenons qu’elle est réflexive.
     a) Donner la matrice booléenne de R.
     b) Donner la fermeture transitive  t(R) de R.
     c) Donner les propriétés de t(R) et conclure.

2) Application : Ordonnancement

Pour accomplir une tâche (globale) certaines tâches intermédiaires doivent être réalisées en respectant des contraintes d’antériorité. Donner des exemples.
On désigne par a, b, c, d, e, f, g, h, i et j ces tâches intermédiaires et soit R la relation d’antériorité représentée par son diagramme sagittal (graphe) :
(x,y)R  si et seulement si la tâche x doit être réalisée avant la tâche y. Convenons qu’elle est réflexive.

On se propose de déterminer un ordre sur les tâches intermédiaires compatible avec l’antériorité.

  a) Si on calcule la fermeture transitive par l’algorithme précédent combien cela nous coûterait-il ?
    b) Réfléchir à un algorithme plus performant en remarquant que ce graphe ne comporte pas de cycle.