Précédent / Suivant / Table des matières

Exercice I :

E={a, b, c, d, e, f, g, h} désigne un ensemble d’émissions de télévision. Le père, la mère et le fils d’une même famille ont chacun classé ces émissions par ordre de préférence :
         père : a, b, c, d, e, f, g, h
         mère : a, c, f, b, d, e, g, h
         fils : a, b, c, e, f, d, h, g
On se propose d’étudier l’existence d’un ordre de préférence pour l’ensemble de la famille. On examinera pour cela les idées suivantes :
1) On dira que l’émission x est préférée à l’émission y si elle l’est pour tous les membres de la famille. Représenter cette relation par son diagramme sagittal et sa matrice booléenne et donner ses propriétés.
2) On dira que l’émission x est préférée à l’émission y si au moins une personne de la famille préfère x à y. Représenter cette relation par son diagramme sagittal et sa matrice booléenne et donner ses propriétés.
3) On dira que l’émission x est préférée à l’émission y si la majorité de la famille préfère x à y. Représenter cette relation par son diagramme sagittal et sa matrice booléenne et donner ses propriétés. Cette dernière méthode mérite une réflexion plus approfondie, pourquoi ? Comparer avec certains systèmes d’élection que vous connaissez.
4) On considère que les membres de la famille ont noté les émissions de 0 à 7 ; on fait le total des notes et on classe les émissions d’après ce total. On obtient :

	a	b	c	d	e	f	g	h
père	7	6	5	4	3	2	1	0
mère	7	4	6	3	2	5	1	0
fils	7	6	5	2	4	3	0	1
Total	21	16	16	9	9	10	2	1

 

Représenter la relation «x a une note supérieure ou égale à y » par son diagramme sagittal et sa matrice booléenne et donner ses propriétés. Que conclure ?

Exercice II :

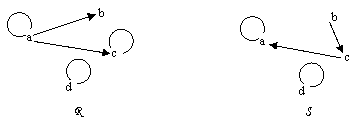E désigne un ensemble fini. R et S sont des relations binaires définies sur E, M et N sont leurs matrices booléennes respectives. Si R S  on notera M ≤ N.
1) Donner la matrice booléenne de : Δ, R^’, R^-1, R S , R ∩S , r(R), s(R), R οS , S οR  , R² et R^k (kN)
Application :

 

 

 

 

 

 

2) Montrer que si R est réflexive alors R  R²  (M ≤ M² ). La réciproque est-elle vraie ?
3) Montrer que R est transitive si et seulement si alors R²  R  (M²≤ M ).
4) Déduire de ce qui précède que si R est un préordre alors R² = R  (M²= M ).