Précédent / Suivant / Table des matières
Travaux Dirigés N°1
Graphes Généralités
EL METHNI M.
Exercice I :
La ville de Koenigsberg (Kaliningrad, région de la Russie frontalière de la Pologne et de la Lituanie) est traversée par le Pregel, qui coule de part et d'autre de l'île de Kneiphof, et possède sept ponts (voir figure). Les habitants (dont Euler) ont pris l'habitude de se promener en traversant tous les ponts. Un habitant désire se promener en partant d'un endroit et y retourner en empruntant une et une seule fois chaque pont.
Modéliser cette situation, y' a-t-il une solution? Pourquoi?

Exercice II : (D’après « fête de la science 2002 »)
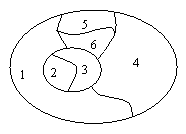
Combien faut-il de couleurs différentes au minimum pour colorier la carte suivante, qui comporte six zones, sans que deux zones limitrophes ne soient de la même couleur ?
Exercice III :
Un concours comporte six épreuves A, B, C, D, E et F. Les candidats doivent choisir un ensemble d’épreuves parmi les suivants : {A, D, E} ; {C, F} ; {B, C} ; {B, E}. Chaque épreuve nécessite une demi-journée.
Quel est le nombre minimal de demi-journées nécessaires pour organiser le concours ?
Exercice IV :
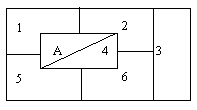
Placer les lettres de B à G dans la grille de façon à ce que deux lettres qui se suivent dans l’alphabet ne se trouvent jamais dans des cases qui se côtoient. Le A est déjà placé.
Exercice V :
Soit T un
ensemble de sept travaux T={t1, t2, t3,
… t7} et M un ensemble de sept machines
M={m1, m2,
m3, … m7}. Chaque travail ti
utilise un certain nombre de machines :
t1 utilise l'ensemble de
machines M1={m1, m3, m5};
t2 utilise l'ensemble de
machines M2={m1, m2, m4};
t3 utilise l'ensemble de
machines M3={m2, m3, m5};
t4 utilise l'ensemble de
machines M4={m2, m4, m7};
t5 utilise l'ensemble de
machines M5={m5, m6, m7};
t6 utilise l'ensemble de
machines M6={ m4, m6, m7};
t7 utilise l'ensemble de
machines M7={ m5, m6, m7}.
Le temps nécessaire à l'exécution de chaque travail ti est le même, mais deux travaux ti et tj
(i≠j) ne peuvent être exécutés
simultanément que s'ils utilisent des machines différentes.
Modéliser cette situation et donner les tâches qui peuvent être exécutées simultanément.
Exercice VI :
Un étudiant décide finalement de préparer son examen
portant sur une matière contenant douze chapitres. Le temps lui manque, il
décide d'étudier deux ou trois chapitres parmi les douze. Ces douze chapitres
ne sont cependant pas tout à fait indépendants :
|
Le chapitre … |
Nécessite la compréhension préalable des chapitres … |
|
1 |
- |
|
2 |
1 |
|
3 |
1 et 2 |
|
4 |
1 et 2 |
|
5 |
1 |
|
6 |
- |
|
7 |
- |
|
8 |
- |
|
9 |
- |
|
10 |
8 |
|
11 |
8 et 10 |
|
12 |
8 et 10 |
Modéliser le problème et aider cet étudiant.