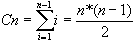
précédent | suivant | table des matières

Evaluation du tri par insertion.

Le pire cas est obtenu avec un tableau en ordre inverse, le meilleur cas avec un tableau déjà ordonné. En pire cas, si la partie déjà ordonnée a m éléments, le nombre de comparaisons à effectuer pour insérer l'élément de rang m+1 est m. Nous pouvons donc écrire :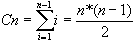

Dans le cas le plus favorable, pour chaque élément à insérer, il n'y a qu'une comparaison. Nous avons alors :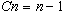

Le calcul du nombre moyen de comparaisons est un peu plus compliqué.

Soit s une permutation de l'ensemble des éléments a_i pour i de 1 à n, tous différents.

Une inversion est un couple (a_i, a_j) de la permutation s tel que : a_i>a_j et i<j. Le nombre d'inversions d'une permutation s est le nombre de couples (a_i, a_j) de la permutation s qui sont des inversions. Il est facile de démontrer que le nombre de comparaisons effectuées lors du tri par insertion est égal au nombre d'inversions de la permutation représentée par le tableau initial. Le nombre moyen de comparaisons lors du tri par insertion, si on fait l'hypothèse que toutes les permutations sont équiprobables et qu'il n'y a pas de doubles, est donc égal au nombre moyen d'inversions pour toutes les permutations de n éléments.

Les n! permutations de n éléments peuvent être rangées en n paquets de (n-1)! éléments chacun. Le premier paquet contient le nième élément de l'ensemble en dernière position ; le deuxième paquet contient le (n-1)ième élément de l'ensemble en dernière position ; Le dernier paquet contient le premier élément de l'ensemble en dernière position.

Exemple : les permutations de (1, 2, 3) sont rangées de la façon suivante :

(1, 2, 3) (2, 1, 3)

(1, 3, 2) (3, 1, 2)

(2, 3, 1) (3, 2, 1)

Pour le premier paquet le nombre d'inversions est égal au nombre d'inversions des (n-1)! permutations de l'ensemble à n-1 éléments, plus le nombre d'inversions générées par l'ajout du dernier élément, soit 0.
Pour le deuxième paquet le nombre d'inversions est égal au nombre d'inversions des (n-1)! permutations de l'ensemble à n-1 éléments, plus le nombre d'inversions générées par l'ajout du dernier élément, soit(n-1) !*1.
...
Pour le dernier paquet le nombre d'inversions est égal au nombre d'inversions des (n-1)! permutations de l'ensemble à n-1 éléments, plus le nombre d'inversions générées par l'ajout du dernier élément, soit (n-1) !*(n-1).

Nous pouvons donc écrire la récurrence suivante sur le nombre d'inversions :

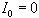
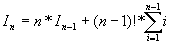
En divisant par n! on obtient le nombre moyen d’inversions, soit :

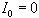
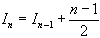
Dont la solution est : 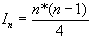qui est dans Q (n2).

Le nombre de transferts est minimum pour un tableau déjà dans l'ordre et maximum pour un tableau en ordre inverse. Dans tous les cas, le nombre de comparaisons et le nombre de transferts sont liés par la relation :

haut de la page