précédent | suivant | table des matières
Pire cas.
L'ordre d'un algorithme de tri par comparaisons est égal à la hauteur de l'arbre de décision associé à cet algorithme. Montrons que l'arbre de décision a une hauteur supérieure ou égale à 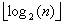 lorsque l'arbre a n feuilles.
lorsque l'arbre a n feuilles.
Démontrons d'abord le lemme suivant : un arbre de 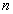 nœuds a au plus
nœuds a au plus 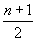 feuilles.
feuilles.
Soit un arbre ayant  nœuds internes et
nœuds internes et 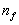 feuilles. Le nombre n de nœuds est :
feuilles. Le nombre n de nœuds est : 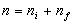
Le nombre c de nœuds de l'arbre étendu est : 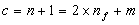 ,
m étant le nombre de nœuds internes ayant une place disponible.
,
m étant le nombre de nœuds internes ayant une place disponible.
Nous avons donc : 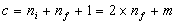 et donc :
et donc : 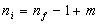
m étant positif ou nul, on en déduit : 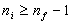
Soit 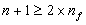
Donc un arbre de n nœuds au total ne peut avoir plus de 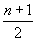 feuilles.
feuilles.
Démontrons maintenant que le nombre de nœuds d'un arbre binaire de hauteur h est au plus 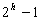
La démonstration se fait par induction sur la hauteur h de l'arbre.
Supposons la relation vraie jusqu'au rang k. Lorsqu'on passe au rang k+1, le nombre maximum de nœuds qui peuvent être ajoutés est égal au nombre de nœuds de l'arbre étendu, soit 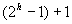
Le nouveau nombre maximum de nœuds est donc : 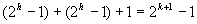
Un arbre binaire de hauteur h a donc au plus 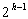 feuilles. Un arbre binaire ayant
feuilles. Un arbre binaire ayant 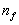 feuilles a donc une hauteur au moins égale à
feuilles a donc une hauteur au moins égale à 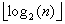 +1.
+1.
Tout arbre de décision valide pour un tri doit avoir au moins 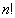 feuilles : en effet il doit pouvoir produire comme verdict chacune des
feuilles : en effet il doit pouvoir produire comme verdict chacune des 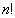 permutations d'un ensemble à n éléments.
permutations d'un ensemble à n éléments.
Pour n grand la formule de Stirling nous donne une approximation de 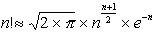 . D'où :
. D'où :
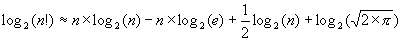
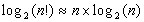
En pire cas, tout algorithme de tri par comparaisons ∈ Ω(n×log(n)).
En moyenne.
Les arbres de décision peuvent aussi servir à étudier la complexité des algorithmes de tri par comparaison en moyenne. Pour cela nous introduisons la notion de hauteur moyenne : La hauteur moyenne d'un arbre est la somme des hauteurs des feuilles divisée par le nombre de feuilles.
Nous cherchons à démontrer la proposition suivante : Tout arbre ayant n feuilles a une hauteur moyenne d'au moins 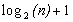 .
.
Supposons qu'il existe des arbres A contenant n feuilles, tel que leurs hauteurs moyennes h(A) soient strictement inférieure à 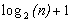 .
.
Parmi les arbres ayant la propriété précédente, 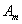 est celui qui contient le moins de nœuds.
est celui qui contient le moins de nœuds.
Trois possibilités se présentent pour l'arbre
|
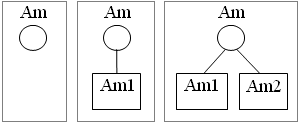
|
Montrons que 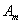 ne peut pas non plus être de la troisième forme :
ne peut pas non plus être de la troisième forme : 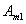 et
et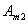 ayant moins de nœuds que
ayant moins de nœuds que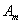 , ils sont forcément tels que :
, ils sont forcément tels que :
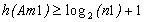
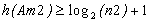
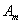 , n1 nombre de feuilles de
, n1 nombre de feuilles de 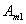 , et n2 nombre de feuilles de
, et n2 nombre de feuilles de 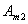 . De plus n1+n2=n. Nous avons donc :
. De plus n1+n2=n. Nous avons donc :
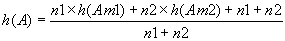
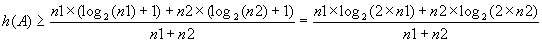
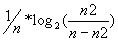 Elle est égale à 0 pour
Elle est égale à 0 pour 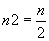 , de plus pour tout
, de plus pour tout 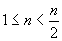 la dérivée est négative ; elle est positive pour tout
la dérivée est négative ; elle est positive pour tout 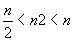
La plus petite valeur de h(A) est atteinte pour 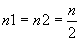 et vaut alors
et vaut alors 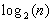 , qui est
, qui est 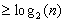 ce qui contredit l'hypothèse de départ.
ce qui contredit l'hypothèse de départ.
En moyenne, tout algorithme de tri par comparaisons ∈ Ω(n×log(n))