correspond à l'arbre : 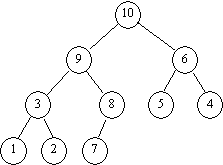
précédent | suivant | table des matières
Imaginé par Williams en 1964 (J.W.J. Williams: Algorithm 232: Heapsort. Communications of the ACM, 7, 6, 347-348 1964), ce tri est aussi appelé tri en tas ou tri maximier.
Ce tri est une accélération du tri par sélection et échange : une organisation préalable de l'ensemble de départ permet d'obtenir une sélection du maximum en un temps qui est dans l'ordre de log2n, ce qui permet à l'algorithme de redevenir optimum.
Le vecteur est considéré comme ayant une structure d'arbre binaire. On fera l’hypothèse que les éléments du tableau ont des indices qui vont de 0 à f (exclu). Un élément d'indice i du vecteur est considéré comme un nœud de l'arbre ; son fils gauche s'il existe se trouve à l'indice 2*i+1 et son fils droit s'il existe se trouve à l'indice 2*i+2. Ce nœud est une feuille si 2*i+1 est supérieur ou égal à f
De plus cet arbre est un maximier c'est à dire qu'il a la propriété d'être ordonné verticalement : chaque nœud contient une valeur supérieure à la valeur contenue dans ses descendants.
exemple :
|
|
correspond à l'arbre : |
La méthode descendre permet de réorganiser un tas dont seule la racine n'est pas à sa place. La racine se trouve à l'indice d.
void descendre( int t [], int d, int f){
int fg, fd, fm;
if(d*2+1 < f) {
fg = 2*d+1;
fd = 2*d+2;
if(fd>=nMax) fm = fg;
else
if (t[fg] > t[fd]) fm = fg; else fm = fd;
if( t[d] > t[fm]) return;
else{
int aux = t[d];
t[d] = t[fm];
t[fm] = aux;
descendre( t, fm, f);
}
}
}
La méthode remonter permet de remonter l'élément de rang n à sa place dans le tas formés par les éléments précédents :
void remonter( int t [], int n){
if(n==1) return;
else if( t[n-1] > t[n/2 - 1]){
int aux = t[n-1];
t[n-1] = t[n/2 - 1];
t[n/2 - 1] = aux;
remonter( t, n/2);
}
}
Pour organiser un tableau en tas, on peut choisir deux solutions :
|
void organiserTas( int t [] ){
for(int i = 2; i < t.length; ++i)
remonter(t, i);
}
|
|
void organiserTasBis( int t [] ){
for(int i = t.length/2; i>= 0; --i)
descendre(t, i, t.length);
}
|
Le tri par tas s’écrit alors :
void trierTas( int t [] ){
organiserTas( t, n);
for( int i = nt.length-1; i>0; --i ){
echanger(t[0], t[i]);
descendre(t, 0);
}