précédent | suivant | table des matières

Algorithme « quick hull ».

Algorithme

Preparata, F. P. and Hong, S. J. (1977). Convex hulls of finite sets of points in two and three dimensions. Communications of the ACM, 20(2), 87-92.

L'algorithme commence par rechercher les deux points d'abcisse la plus grande et d'abcisse la plus petite. La droite qui rejoint ces deux points partage l'ensemble des points en deux ensembles.
Dans chacun des ensembles, on cherche le point le plus élogné de la droite P1P2, soit H ce point. On obtient alors les deux ensembles de points E1 et E2, avec lesquels on recommence cette opération. L'un ou l'autre de ces deux ensembles peut être vide

void quickHull(ArrayList<Point> lp, ArrayList<Point> env){
   env.clear();
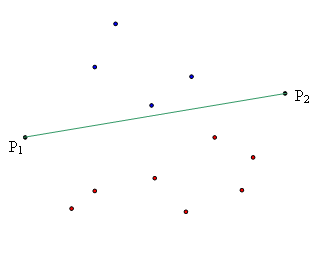
   // recherche du point le plus à droite, le plus à gauche,
   Point pDroite= (Point)lp.get(0);
   Point pGauche= (Point)lp.get(0);
   for( int i = 1; i < lp.size(); ++i) {
      Point p = ((Point)lp.get(i));
      if(p.x>pDroite.x) pDroite = p;
      else if(p.x < pGauche.x) pGauche = p;
   }
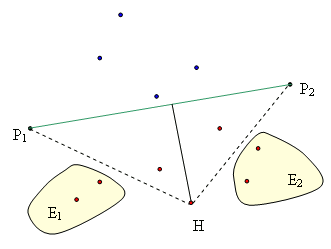
   // Division en deux sous ensembles
   // ceux qui sont d'un coté et ceux qui sont de l'autre
   ArrayList<Point> e1 = new ArrayList<Point>();  
   ArrayList<Point> e2 = new ArrayList<Point>();
   if(pDroite.x==pGauche.x){ // points alignés verticalement ...
         //pGauche est le + petit y et pDroite le plus Grand y
         for( int i = 0; i < lp.size(); ++i){
            if(lp.get(i).y < pGauche.y)  pGauche = lp.get(i);
            else if(lp.get(i).y>pDroite.y) pDroite = lp.get(i);
         }
    }	
   for( int i = 0; i< lp.size(); ++i) {
      Point p = ((Point)lp.get(i));
      if(distance(pGauche, p)!=0 && distance(pDroite, p)!=0){
         // p n'est pas pGauche, ni pDroite
         if( surface(pDroite, pGauche, p) < 0 )  e1.add(p);
         if( surface(pGauche, pDroite, p) < 0 )  e2.add(p);
      }
   }
   env.clear();
   env.add(pDroite);  quickHullBis(pDroite, pGauche, e1, env);
   env.add(pGauche);  quickHullBis(pGauche, pDroite, e2, env);
}

void quickHullBis(Point p1, Point p2, ArrayList<Point> e, ArrayList<Point> enveloppe){
     if( e.isEmpty() ) return;
     if( e.size()==1){ enveloppe.add(e.get(0));  return; }
     // recherche du point de e le plus éloigné du segment p1, p2
     double d = distance(p1, p2);
     Point pM = ((Point)e.get(0)) ;
     double dM = 2*Math.abs(surface(p1, p2, pM)/d);
     for( int i = 1; i < e.size(); ++i){
         Point p = ((Point)e.get(i));
         double dl = 2*Math.abs(surface(p1, p2, p)/d);
         if(dl > dM){
            pM = p;
            dM = dl;
         }
     }
     // Division de e en e1, e2
     ArrayList<Point> e1 = new ArrayList<Point>();    
     ArrayList<Point> e2 = new ArrayList<Point>();
     for( int i = 0; i< e.size(); ++i) {
       Point p = ((Point)e.get(i));
        if( distance(p, pM)!=0 ){
           if( surface(p1, pM, p) < 0 )  e1.add(p);
           if( surface(pM, p2, p) < 0 )  e2.add(p);
        }
     }
     quickHullBis(p1, pM, e1, enveloppe);
     enveloppe.add(pM);
     quickHullBis(pM, p2, e2, enveloppe);
}

Estimation

Dans le meilleur des cas la complexité de l'algorithme est de l'ordre de n×log(n) mais peut dans ceratins cas être de l'ordre de n².

1. quickHullBis
   Soit n le nombre de points de e :
   • La recherche du point le plus éloigné du segment P₁P₂ a un coût de l’ordre de n.
   • La partition a un coût de l’ordre de n.
   • Si la partition fabrique 3 parties de taille égales le coût est donné par la récurrence :
        t₀ =1
        t₁ =1
        t_n = 2×t_n/3+n
     
   • Si la partition fabrique 2 parties de taille égales sans exclure de points, le coût est donné par la récurrence :
        t₀ =1
        t₁ =1
        t_n = 2×t_n/2+n
     
   • Si la partition fabrique 1 partie contenant tous les points sauf le point H, le coût est donné par la récurrence :
        t₀ =1
        t₁ =1
        t_n = t_n-1+n
     
2. QuickHull
   • La recherche des points haut et bas a un coût de l’ordre de n.
   • La partition a un coût den.
   • Le coût total est 2×n plus 2 fois le coût de quickHullBis.

haut de la page