précédent | suivant | table des matières
Algorithme
On calcule tous les points strictement intérieurs à l’ensemble de points : les points de l’ensemble qui ne sont pas strictement à l’intérieur sont des points de l’enveloppe.
Un point p est strictement à l’intérieur de l’ensemble, s’il existe 3 autres points (p0, p1, p2) qui forme un triangle contenant le point p.
Le calcul de la surface d’un triangle donné par 3 points (p0, p1, p2), s’exprime de la façon suivante : 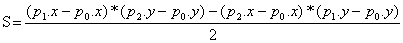 , cette surface est <0 si lors du parcours (p0, p1, p2) on tourne dans le sens inverse des aiguilles d’une montre et <0 dans le cas contraire. Un point p est à l’intérieur du triangle (p0, p1, p2), si et seulement si les surfaces des triangles (p0, p, p1), (p1, p, p2) et (p2, p, p0)sont toutes de même signe.
, cette surface est <0 si lors du parcours (p0, p1, p2) on tourne dans le sens inverse des aiguilles d’une montre et <0 dans le cas contraire. Un point p est à l’intérieur du triangle (p0, p1, p2), si et seulement si les surfaces des triangles (p0, p, p1), (p1, p, p2) et (p2, p, p0)sont toutes de même signe.
Le calcul de l’enveloppe convexe s’exprime simplement en énumérant tous les points et tous les triangles :
void algoNaif(ArrayList<Point> lp, ArrayList<Point> env){
// un point est sur l'enveloppe s'il n'est à l'intérieur
// d'aucun triangle formé par les autres points
env.clear();
ArrayList nonEnveloppe = new ArrayList<Point>();
for( int i = 0; i<lp.size(); ++i)
for( int j = i+1; j<lp.size(); ++j){
for( int k = j+1; k<lp.size(); ++k){
for( int l = 0 ; l<lp.size(); ++l){
if(l!=i && l!=j && l!=k) {
if(interieur( lp, i, j, k, l)){ // le point l est-il à l'intérieur du triangle (i, j, k)
nonEnveloppe.add(lp.get(i));
}
}
}
}
}
for( int i = 0; i < lp.size(); ++i)env.add(lp.get(i));
env.removeAll(nonEnveloppe);
}
Il faut remarquer que, en plus de sa lenteur, cet algorithme ne donne pas l'ordre sur les points de l'enveloppe qu'il faudrait utiliser pour tracer cette enveloppe !
Estimation
Soit n le nombre de points. Evaluons le nombre d’appels de la méthode interieur :
N=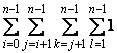
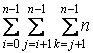
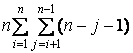 =
=