précédent | suivant | table des matières

Algorithme de Graham.

1Algorithme

Cet algorithme doit son nom à Ronald Graham, qui a publié l'algorithme original en 1972.Graham, R.L. (1972). 
An Efficient Algorithm for Determining 
the Convex Hull of a Finite Planar Set. 
Information Processing Letters 1, 132-133

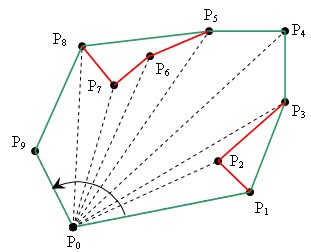
Soit Pb le point le plus bas. On commence par trier les points Pi par ordre croissant des angles que forme le segment PiPb avec l’horizontale, les points alignés étant ordonnés par ordre croissant des abscisses. Puis on construit l’enveloppe convexe comme une pile : le dernier élément et le premier élément de l’ensemble trié des points sont empilés. Soient P0 et P1 les éléments en sommet de pile ( P1 est au sommet ). Puis on parcourt tous les éléments de l’ensemble trié à partir du second : soit P2 cet élément :

  1. Si P0P1P2 tourne à gauche, on peut avancer : P2 est empilé.
  2. Si P0P1P2 tourne à droite, alors P1 n’est pas sur l’enveloppe convexe, on l’enlève de la pile et on recommence 2. avec les deux points sommet de pile et P2.
 graham 
void graham(ArrayList<Point> lpp, ArrayList<Point> env){
   if(env == null) return;
   if( lpp.size()<=3) { env.addAll(lpp); return;}
   ArrayList lp= (ArrayList)lpp.clone();
   env.clear();
   // recherche du point le plus bas et le plus à gauche
   Point pBasGauche = (Point)lp.get(0);
   int iBasGauche = 0;
   for( int i = 1; i < lp.size(); ++i) {
      Point p = ((Point)lp.get(i));
      if(p.y > pBasGauche.y || (p.y==pBasGauche.y && p.x < pBasGauche.x)){
          pBasGauche = p;
          iBasGauche = i;
      }
   }
   // ordonner les points par angle croissant
   lp.remove(iBasGauche);
   Collections.sort(lp ,new Comparaison(pBasGauche));
   lp.add(0, pBasGauche);
   // calcul de l'enveloppe
   Point p0, p1;
   p0 = (Point)lp.get(lp.size()-1);
   p1 = (Point)lp.get(0);
   env.add(p0);env.add(p1);
   for( int i = 1; i < lp.size(); ++i) {
      Point p2 = (Point)lp.get(i);
      for( ; ;){
          p0 = (Point)env.get(env.size()-2);
          p1 = (Point)env.get(env.size()-1);
          // si ça tourne pas dans le bon sens on enlève
          if(surface(p0, p1, p2) >= 0 && env.size()>1){
             env .remove(env.size()-1);
          }
          else break;
      }
      env.add(p2);
   }
}

2Estimation

Le tri a un coût de n×log(n) , puis l’extraction de l’enveloppe un coût de n×(1+m), m étant le nombre moyen de retraits de la pile. Le nombre de retraits moyen est inférieur au nombre de points, donc l’extraction a un coût de l’ordre de n.

haut de la page