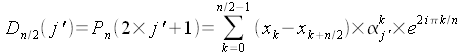précédent |
suivant |
table des matières
Transformée de Fourier rapide.
|
Quelques références :  et sur Wikipédia et sur Wikipédia
Une application de démonstration en une dimension, et en deux dimensions.
Il existe de nombreuses façons de représenter un polynôme de degré n ; parmi ces représentations deux vont nous
intéresser :
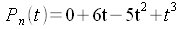
- Un polynôme peut être décrit par la liste ordonnée de ses
coefficients : Pn(t) = (0, 6, -5, 1)
- Un polynôme peut être représenté par la liste de ses valeurs
en n points distincts. Pour l'exemple précédent,
on aura les deux possibilités suivantes :
- Pn(t) = (Pn(0), Pn(1), Pn(2), Pn(3) ) = (0, 2, 0, 0)
- Pn(t) = (Pn(1), Pn(i), Pn(-1), Pn(-i) ) avec i tel que i2=-1
Pn(t)= (2, 5+5*i, -12, 5-5*i)
|
|
 Définition.
Définition.
La transformée de Fourier du polynôme de degré n décrit
par la liste ordonnée de ses coefficients, est le même
polynôme décrit par la liste de ses valeurs pour les n
racines nième de 1.
Soit j
une racine nième de 1 pour j
{0, 1, ... n-1}, nous avons :
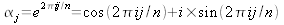
La transformée de Fourier du polynôme de coefficients (x0,
x1, ... xn-1)
est donnée par la liste telle
que :
telle
que : 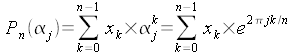
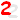 Algorithme de Cooley-Tukey.
Algorithme de Cooley-Tukey.
Cooley, J.W. et Tukey, J.W 1965
An algorithm for machine calculation of complex Fourier series,
Mathematics of computation 19, 90, pp 297-301
Une première idée pour calculer la transformée de Fourier d'un
polynôme est d'utiliser l'algorithme du schéma de
Horner : cet algorithme nécessite (n2)
opérations élémentaires. Nous allons voir
comment la transformée de Fourier peut être calculée
plus rapidement.
Supposons que n soit une puissance de 2 : n=2m
Nous avons alors pour chaque j de 0 à n-1 :
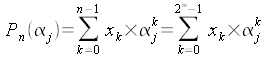
En séparant les termes de rang pair des termes de rang impair dans la somme
ci-dessus, nous obtenons :
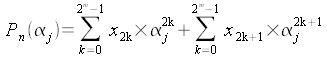
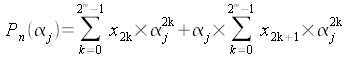
Or 
-
Pour j < n / 2
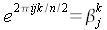 qui est une racine (n / 2)ième de
l'unité.
qui est une racine (n / 2)ième de
l'unité.
Nous pouvons donc écrire :
(1) 
- Pour j n / 2.
Montrons que si j
est une racine nième de l'unité, pour
jn on
a : j
= j%n
On a j = j % n + n(j
/ n)
Donc :
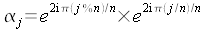

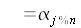
La relation (1) s'écrit alors de la façon suivante :
(1) 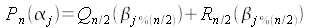
Dans la relation ci-dessus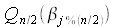 est
la transformée de Fourier des termes de rang pair, et
est
la transformée de Fourier des termes de rang pair, et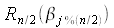 est
la transformée de Fourier des termes de rang impair.
est
la transformée de Fourier des termes de rang impair.
Nous en déduisons l'algorithme récursif suivant :
Complex [] fft ( Complex x[] ){
int n = x.length;
Complex res[] = new Complex[n];
Complex[] pair, impair, u, v ;
int i, i1;
double alphai, alpha;
if(n == 1) res[0] = x[0];
else{
pair = new Complex [n/2];
impair = new Complex [n/2];
for( i = 0; i<n/2 ; ++i){
pair[i] = x[2*i];
impair[i] = x[2*i+1];
}
u = fft(pair);
v = fft(impair);
alpha = 2*Math.PI/n;
for( i = 0; i<= n-1; ++i){
alphai = alpha*i;
i1 = i % ( n/2 );
Complex tau = new Complex (Math.cos(alphai), Math.sin(alphai));
res[i]= u[i1].add(tau .mul(v[i1]));
}
}
return res;
}
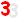 Transformée de Fourier inverse.
Transformée de Fourier inverse.
Si les ordinateurs préfèrent travailler avec une représentation des
polynômes par transformée de Fourier, l'être
humain préfère généralement travailler
sur une représentation des polynômes par la liste de ses
coefficients. Le problème se pose donc de retrouver la liste
des coefficients à partir de la transformée de Fourier.
Soit A la matrice dont le terme de ligne i
et de colonne k est ik,
X le vecteur colonne dont le terme de ligne i est xi,
et FFT le vecteur colonne dont le terme de ligne i est
Pn(i).
Nous pouvons écrire :

Soit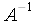 la matrice inverse de A si elle existe, nous avons alors :
la matrice inverse de A si elle existe, nous avons alors :
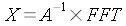
Montrons que
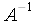 est
la matrice dont le terme de ligne i et de colonne k est
est
la matrice dont le terme de ligne i et de colonne k est
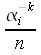
La matrice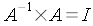 est
la matrice dont le terme de ligne i et de colonne j est
est
la matrice dont le terme de ligne i et de colonne j est

Suivant les valeurs relatives de i et j on a :
- i = j
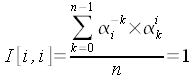 car
car 
- i < j
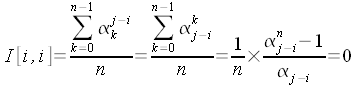
- i > j
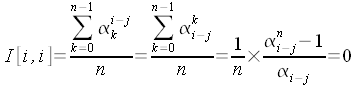
L'algorithme de calcul de la transformée de Fourier inverse se déduit de
l'algorithme de calcul de la transformée de Fourier en
changeant uniquement le signe de calcul du sinus. De plus il faut
prendre soin, lorsque le calcul est terminé, de diviser tous
les éléments du tableau RES par n .
Complex [] fftInvA ( Complex x[] ){
int n = x.length;
Complex res[] = new Complex[n];
Complex[] pair, impair, u, v ;
int i, i1;
double alphai, alpha;
if(n == 1) res[0] = x[0];
else{
pair = new Complex [n/2];
impair = new Complex [n/2];
for( i = 0; i<n/2 ; ++i){
pair[i] = x[2*i];
impair[i] = x[2*i+1];
}
u = fft(pair);
v = fft(impair);
alpha = 2*Math.PI/n;
for( i = 0; i<= n-1; ++i){
alphai = alpha*i;
i1 = i % ( n/2 );
Complex tau = new Complex (Math.cos(alphai), - Math.sin(alphai));
res[i]= u[i1].add(tau .mul(v[i1]));
}
}
return res;
}
Complex [] fftInv ( Complex[] x){
Complex n = new Complex(x.length, 0) ;
Complex [] res = fftInvA(x);
for(int i=0 ; i<x.length ;++i) res[i] = res[i].div(n) ;
return res;
}
 Evaluation de l'algorithme.
Evaluation de l'algorithme.
La complexité temporelle de l'algorithme de la transformée de Fourier est
donnée par la récurrence suivante :
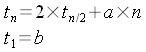
En effet le calcul de la transformée de Fourier pour n éléments
nécessite le calcul de 2 transformées de Fourier pour n/2 éléments plus un temps proportionnel à
n pour séparer le tableau initial en deux sous tableaux et pour réunir les deux résultats.
La résolution de la récurrence précédente fournit la solution
pour tn :
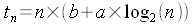
La complexité temporelle de la transformée de Fourier pour un polynôme
de degré n est donc : 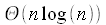
Pour calculer la complexité spatiale de la transformée de Fourier nous
ne nous occuperons que des tableaux déclarés dans la
procédure, en laissant de coté l'espace occupé
par la pile servant à gérer les appels récursifs.
La complexité spatiale de la transformée de Fourier est
alors donnée par la récurrence :
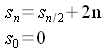
Dont la solution est 4×(n-1).
C'est ce «gaspillage» de place qui nous incite à étudier une version
itérative de l'algorithme.
 Transformée de Fourier itérative.
Transformée de Fourier itérative.
Les deux appels récursifs qui démarrent l'algorithme de la transformée
de Fourier ne servent qu'à réorganiser le vecteur des
coefficients à chaque niveau dans l'arbre. La concaténation
des vecteurs pair et impair à chaque niveau permet d'obtenir
la permutation des coefficients réalisée par les appels
récursifs.
exemple :
Pour 2m = n = 8 nous avons :
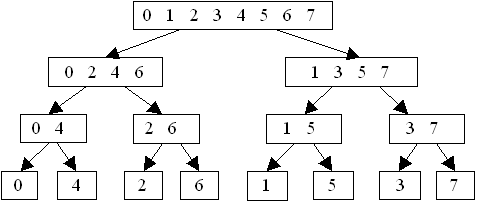
Si T est le tableau initial, et Tf le tableau final, nous remarquons que :
T[i] = Tf[j] et
j est l'image miroir de la représentation de i
en numération binaire avec m bits
L'action de
recombinaison qui suit les appels récursifs consiste à
reconstituer le vecteur RES à partir des vecteurs U
et V. Il s'agit du parcours de l'arbre précédent
des feuilles vers la racine, et niveau par niveau.
A chaque niveau il y a
m recombinaisons. Au départ m vaut n / 2,
puis à l'étape suivante m div 2, et ainsi de
suite jusqu'à une seule recombinaison élémentaire
qui fournit le résultat.
Dans l'algorithme
suivant la fonction inverse(i, m) calcule l'inverse dans la
représentation en binaire sur m bits de i.
La fonction suivante
effectue la «fusion» de deux transformées
de Fourier de n éléments en une transformée
de Fourier de 2×n
éléments.
void fusionElem( int lg, int deb, Complex x[], Complex y[]){
int j, j1, j2, j3;
double omegai, omega ;
omega = Math.PI/lg;
for( j = 0; j<2*lg; ++j){
omegai = omega*j;
Complex tau = new Complex(Math.cos(omegai), Math.sin(omegai));
j1 = deb + j;
j2 = deb + j % lg;
j3 = j2 + lg;
y[j1] = x[j2].add( tau.mul(x[j3]));
}
}
La fonction suivante effectue m fusions élémentaires à
chacune des m étapes de l'algorithme.
void fusion ( int n, int p2, Complex []x, Complex []res){
int i, k, p2i;
p2i=1;
i = 1;
while(true){
if(i>p2){
for(k = 0; k<2i; ++k) res[k] = x[k];
break;
}
p2i *= 2;
n /= 2;
for(k = 0; k<n; ++k) fusionElem(p2i / 2, k*p2i, x, res);
i=i+1;
if(i>p2) break;
p2i *= 2;
n /= 2;
for(k = 0; k<n; ++k) fusionElem(p2i / 2, k*p2i, res, x);
i=i+1;
}
}
Enfin la fonction suivante calcule la transformée de Fourier à partir du
tableau des coefficients.
Complex[] fftIter( Complex[] x){
int p2, n1;
int n = x.length;
Complex [] y = new Complex[n];
for( int i = 0; i<n; ++i) y[i] = x[i];
Complex [] res = new Complex[n];
p2 = 0; n1 = n;
while (n1!=0){ p2 = p2+1; n1 = n1 / 2 ;} --p2;
for( int i = 0; i<n; ++i) res[i] = y[inverse(i, p2)];
for( int i = 0; i<n; ++i) y[i] = res[i];
fusion( n, p2, y, res);
return res;
}
 Application à la multiplication des polynômes.
Application à la multiplication des polynômes.
Soient Pn1
et Pm2 deux polynômes
de degrés respectifs n et m :
Pn1(t)
= (x0, x1, ... xn)
Pm
2(t) = (y0,
y1, ... ym)
Le produit est un polynôme de degré n+m :
Pn+m(t) = Pn1(t)
× Pm 2(t)
Le calcul direct de ce polynôme produit nécessite (n×m)
opérations élémentaires.
L'algorithme de la transformée de Fourier permet d'accélérer ce processus.
Supposons que n>m, nous pouvons écrire : 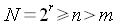
Les deux polynômes P1 et P2 s'écrivent
alors de la façon suivante :
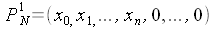
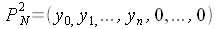
Le polynôme produit des deux polynômes P1 et P2
peut se calculer en utilisant la transformée de Fourier et son inverse :
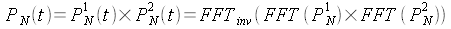
Le temps de calcul devient (N×log(N)).
Exemple : Soient
les polynômes :
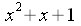 et
et .
La représentation de ces polynômes aux points 0, 1, 2,
et 3 est (1, 3, 7, 13) et (2, 4, 6, 8). Le produit des deux polynômes
est
.
La représentation de ces polynômes aux points 0, 1, 2,
et 3 est (1, 3, 7, 13) et (2, 4, 6, 8). Le produit des deux polynômes
est
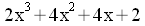 dont
la représentation aux points 0, 1, 2, et 3 est le produit des
représentations, soit : (2, 12, 42, 104)
dont
la représentation aux points 0, 1, 2, et 3 est le produit des
représentations, soit : (2, 12, 42, 104)
 Application à la multiplication des nombres entiers.
Application à la multiplication des nombres entiers.
Un nombre entier a peut s’écrire : où
B est la base. Pour multiplier deux nombre entiers a et
b, on peut suivre l’algorithme suivant :
où
B est la base. Pour multiplier deux nombre entiers a et
b, on peut suivre l’algorithme suivant :
- Calculer la transformée de Fourier de a, puis de b.
- Calculer le produit terme à terme des deux transformées
- Puis calculer la transformée inverse.
Les calculs de la transformée de Fourier se font avec des complexes et donc ne
sont pas exacts. Si les erreurs sur chaque chiffre sont inférieures
à ½ , il suffit d’arrondir chaque réel
obtenu.
On démontre que l’erreur faite sur les calculs est inférieure à
 où ε est
la précision machine ( ≈
10-16
pour les double et ≈
10-7
pour les float). En pratique l’erreur est inférieure à
où ε est
la précision machine ( ≈
10-16
pour les double et ≈
10-7
pour les float). En pratique l’erreur est inférieure à
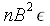 .
.
 Une autre façon de calculer la
Transformée.
Une autre façon de calculer la
Transformée.
La transformée de Fourier peut se calculer en séparant les n / 2
premiers éléments des n / 2 éléments
suivants dans le tableau initial des coefficients. Dans la méthode
précédente on séparait les rangs pairs des rangs impairs.


Deux cas se présentent :
- Pour j
pair, j=2*j', donc
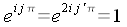 et
et
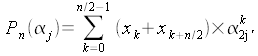 Donc
les termes de rang pair de la transformée de Fourier du
polynôme initial, sont les termes de la transformée de
Fourier du polynôme suivant :
Donc
les termes de rang pair de la transformée de Fourier du
polynôme initial, sont les termes de la transformée de
Fourier du polynôme suivant : 
- Pour j impair, j=2*j'+1, donc
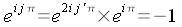 et
et 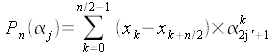 Donc
les termes de rang impair de la transformée de Fourier du
polynôme initial, sont les termes de la transformée de
Fourier du polynôme suivant :
Donc
les termes de rang impair de la transformée de Fourier du
polynôme initial, sont les termes de la transformée de
Fourier du polynôme suivant : 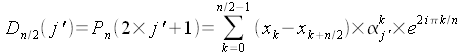
void fftIterBis(int n, Complex x[], Complex[] res, int deb, int pres) {
Complex[] c, d;
int k;
double alpha;
c = new Complex[n / 2];
d = new Complex[n / 2];
if (n == 1)
res[deb] = x[0];
else {
for (k = 0; k <n / 2; ++k) {
c[k] = x[k].add(x[k + n / 2]);
alpha = 2 * k * Math.PI / n;
Complex tau = new Complex(Math.cos(alpha), Math.sin(alpha));
d[k] = (x[k].sub(x[k + n / 2])).mul(tau);
}
fftIterBis(n / 2, c, res, deb, 2 * pres);
fftIterBis(n / 2, d, res, deb + pres, 2 * pres);
}
}
public Complex[] fftIterBis(Complex x[]) {
Complex res[] = new Complex[x.length];
fftIterBis(x.length, x, res, 0, 1);
return res;
}
haut de la page
 et sur Wikipédia
et sur Wikipédia![]()
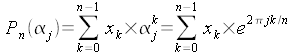
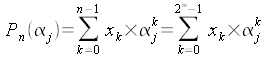
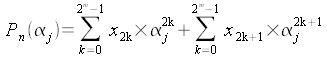
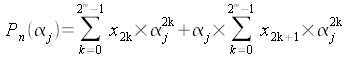

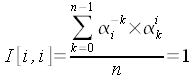 car
car 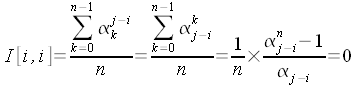
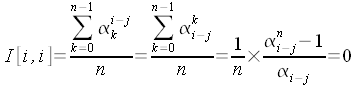
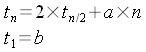
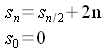

 où
B est la base. Pour multiplier deux nombre entiers a et
b, on peut suivre l’algorithme suivant :
où
B est la base. Pour multiplier deux nombre entiers a et
b, on peut suivre l’algorithme suivant : 

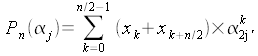 Donc
les termes de rang pair de la transformée de Fourier du
polynôme initial, sont les termes de la transformée de
Fourier du polynôme suivant :
Donc
les termes de rang pair de la transformée de Fourier du
polynôme initial, sont les termes de la transformée de
Fourier du polynôme suivant : 
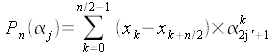 Donc
les termes de rang impair de la transformée de Fourier du
polynôme initial, sont les termes de la transformée de
Fourier du polynôme suivant :
Donc
les termes de rang impair de la transformée de Fourier du
polynôme initial, sont les termes de la transformée de
Fourier du polynôme suivant :